Quadratic equations: Section 2
Proof of the quadratic formula
IN LESSON 18, we saw a technique called completing the square. We will now see how to apply it to solving a quadratic equation.
Completing the square
If we try to solve this quadratic equation by factoring,
| x² + 6x + 2 | = | 0 |
| we cannot. Therefore, we complete the square. That means to make the quadratic into the form | ||
| a² + 2ab + b² | = | (a + b)². |
The technique is valid only when 1 is the coefficient of x².
| 1) | Transpose the constant term to the right: |
x² + 6x = −2
| 2) | Add a square number to both sides. Add the square of half the coefficient of x. In this case, add the square of 3: |
x² + 6x + 9 = −2 + 9
The left-hand side is now the perfect square of (x + 3).
(x + 3)² = 7
3 is half of the coefficient 6.
This equation has the form
| a² | = | b | |
| which implies | |||
| a | = | ± |
|
| Therefore, | |||
| x + 3 | = | ± |
|
| x | = | −3 ± |
|
That is, the solutions to
x² + 6x + 2 = 0
are the conjugate pair,
−3 + ![]() , −3 −
, −3 − ![]() .
.
For a method of checking these roots, see Lesson 10 of Topics in Precalculus,
In Lesson 18, there are examples and problems in which the coefficient of x is odd. Also, some of the quadratics below have complex roots, and some involve simplifying radicals.
Problem 6. Solve each quadratic equation by completing the square.
To see the answer, pass your mouse from left to right
over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | x² − 2x − 2 | = | 0 | b) | x² + 4x − 6 | = | 0 | |
| x² − 2x | = | 2 | x² + 4x | = | 6 | |||
| x² − 2x + 1 | = | 2 + 1 | x² + 4x + 4 | = | 6 + 4 | |||
| (x − 1)² | = | 3 | (x + 2)² | = | 10 | |||
| x − 1 | = | ± |
x + 2 | = | ± |
|||
| x | = | 1 ± |
x | = | −2 ± |
|||
| c) | x² − 4x + 13 | = | 0 | d) | x² + 6x + 29 | = | 0 | |
| x² − 4x | = | −13 | x² + 6x | = | −29 | |||
| x² − 4x + 4 | = | −13 + 4 | x² + 6x + 9 | = | −29+ 9 | |||
| (x − 2)² | = | −9 | (x + 3)² | = | −20 | |||
| x − 2 | = | ±3i | x + 3 | = | ± |
|||
| x | = | 2 ± 3i | x | = | −3 ± 2i |
|||
| e) | x² − 5x − 5 | = | 0 | f) | x² + 3x + 1 | = | 0 | |
| x² − 5x | = | 5 | x² + 3x | = | −1 | |||
| x² − 5x + 25/4 | = | 5 + 25/4 | x² + 3x + 9/4 | = | −1 + 9/4 | |||
| (x − 5/2)² | = | 5 + 25/4 | (x + 3/2)² | = | − 1 + 9/4 | |||
| x − 5/2 | = | ± |
x + 3/2 | = | ± |
|||
| x | = | x | = | |||||
The quadratic formula
Here is the quadratic formula -- which is proved by completing the square! In other words, the quadratic formula completes the square for us.
Theorem. If
ax² + bx + c = 0,
Theorem. then
![]()
We will prove this below.
Example 4. Use the quadratic formula to solve this quadratic equation:
3x² + 5x − 8 = 0
Solution. We have: a = 3, b = 5, c = −8.
Therefore, according to the formula:
| x | = | |
| = | ||
| = | ||
| = | ||
That is,
| x | = | −5 + 11 6 |
or | −5 − 11 6 |
| x | = | 6 6 |
or | −16 6 |
| x | = | 1 | or − | 8 3 |
. |
These are the two roots. And they are rational. This tells us that we could have solved the equation by factoring, which is always the simplest method.
| 3x² + 5x − 8 | = | (3x + 8)(x − 1) | ||
| x | = | − | 8 3 |
or 1. |
Problem 7. Use the quadratic formula to find the roots of each quadratic.
a) x² − 5x + 5
a = 1, b = −5, c = 5.
| x | = | = | = |
b) 2x² − 8x + 5
a = 2, b = −8, c = 5.
| x | = | |||||||
| = | = | = | = | 2 + ½ |
||||
c) 5x² − 2x + 2
a = 5, b = −2, c = 2.
| x | = | |||||||
| = | = | = | 2 ± 6i 10 |
= | 1 ± 3i 5 |
|||
The discriminant
The radicand b² − 4ac is called the discriminant. If the discriminant is
| a) Positive: | The roots are real and conjugate. |
| b) Negative: | The roots are complex and conjugate. |
| c) Zero: | The roots are rational and equal -- i.e. a double root. |
Proof of the quadratic formula
To prove the quadratic formula, we complete the square. But to do that, the coefficient of x² must be 1. Therefore, we will divide both sides of the original equation by a:
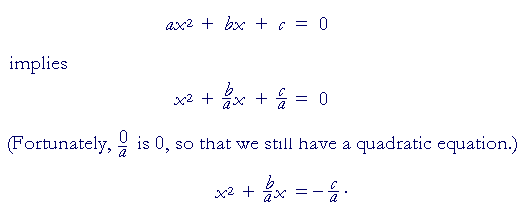
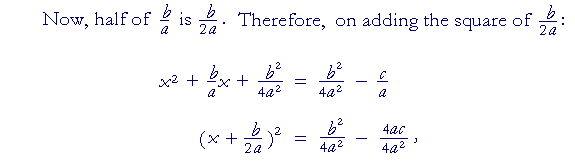
on multiplying both c and a by 4a, thus making the denominators the same (Lesson 23),
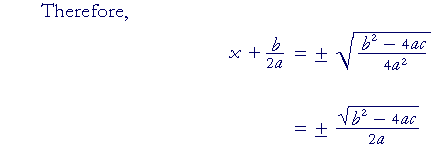
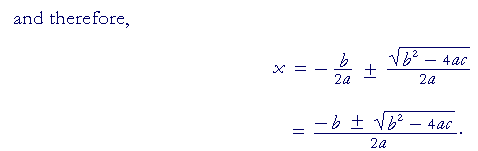
This is the quadratic formula.
Section 3: The graph of y = A quadratic
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com