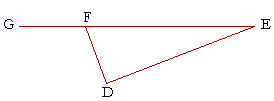
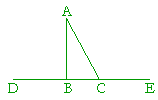Book I.  Proposition 16

Problems

Back to Proposition 16.

1.  In triangle DEF, side EF has been extended to G.

1.  a)  Name that exterior angle.

To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!

Angle GFD.

1.  b)  Name the two angles that are interior and opposite to it.

Angles FED, EDF.

1.  c)  Name the angle that is adjacent to it.

Angle DFE.

2.   a)  State the hypothesis of Proposition 16.

One of the sides of a triangle is extended.

2.  b)  State the conclusion.

The exterior angle is greater than either of the opposite interior angles.

2.  c)  Practice Proposition 16.

3.   Prove:  From one point it is not possible to draw to the same straight line
3.   three straight lines equal in length.

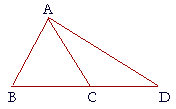
That is, the straight lines AB, AC, AC cannot be equal in length,
if B, C, D are in a straight line.

[Hint:  Use the indirect method.  Assume those lines are equal, and show how that leads to a contradiction.]

If AB is equal to AC, then in triangle ACB,
angle ACB is equal to angle ABC.
And if AB is equal to AD, then angle ADB is also equal to angle ABC,
and therefore to angle ACB.
Therefore in triangle ACD, the exterior angle ACB
is equal to the opposite interior angle ADC; which is impossible.
Therefore the straight lines AB, AC, AD cannot all be equal in length.

4.   Prove:  There is only one perpendicular to a straight line from a point not on it.

From the point A there is only one perpendicular AB to the straight line DE.

For suppose that AC is also a perpendicular to DE.
Then the right angle ACE is equal to the right angle ABC.
That is, in triangle ABC, the exterior angle ACE is equal to the opposite interior angle ABC; which is impossible.
Therefore AC is not perpendicular to DE.
From the point A,  AB is the only one.

5.   a)  State the hypothesis of Proposition 17.

This figure is a triangle.

5.  b)  State the conclusion.

And two of its angles are together less than two right angles.

5.  c)  Practice Proposition 17.

Next proposition

Previous proposition

Table of Contents | Introduction | Home

---

Please make a donation to keep TheMathPage online.
Even $1 will help.

---

Copyright © 2006-2007 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com