THE SIDES AND ANGLES OF A TRIANGLE

Book I. Propositions 18 and 19

THE STUDENT by now must have some appreciation of what is involved in a logical theory. Each proposition must wait its turn, for each depends on some previous proposition or first principle -- even the most obvious.

Consider for example the following:

Any two sides of a triangle are together
greater than the remaining side.

In other words, a straight line is the shortest distance between two points!

If anyone wanted to ridicule mathematics for its insistence on the axiomatic method of orderly proof, this theorem offers a wide target. In fact, the Epicureans (those Athenian free-thinkers, who defined philosophy as the art of making life happy) did exactly that. They said that this theorem required no proof, and was known even to an ass. For if hay were placed at one vertex, they argued, and an ass at another, the poor dumb animal would not travel two sides of the triangle to get his food, but only the one side which separated them.

Such is the scorn that the true philosopher must bear! And what can the mathematician do but to point out, patiently, that mathematics as a logical science relies on deduction from first principles. Those principles moreover should be as few in number as possible — whatever can be proved should be. That is the intellectual sport.

This proposition -- Any two sides of a triangle are together greater than the remaining side -- is Euclid's Proposition 20. And to prove it he first had to prove

Proposition 19. A greater angle of a triangle is opposite a greater side.

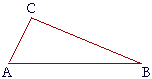
If angle A is greater than angle B, then side CB is greater than side CA.

And to prove that he first had to prove

Proposition 18. A greater side of a triangle is opposite a greater angle.

And to prove that he had to prove Proposition 16, which we just saw.

This is what one has to go through to form a proof!

(Proposition 17 was not needed: Any two angles of a triangle are together less than two right angles. That will be Problem 4.)

Here, then, are Propositions 18 and 19.

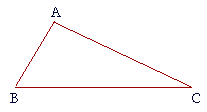
PROPOSITION 18. THEOREM

A greater side of a triangle is opposite a greater angle.

Let ABC be a triangle in which side AC is greater than side AB;

then angle ABC is also greater than angle BCA.



For, since AC is greater than AB, make AD equal to AB,	(I. 3)

and draw DB.

Then in triangle DBC,

the exterior angle ADB is greater than the opposite interior angle BCD.	(I. 16)

But since side AD is equal to side AB,

angle ABD is equal to angle ADB;	(I. 5)

therefore angle ABD is also greater than angle BCD.

Therefore angle ABC is much greater than angle BCA.	(Axiom 5)

Therefore, a greater side etc. Q.E.D.

We have proved this proposition directly. But we must prove the next proposition indirectly, and to do that we have to cite the previous one.

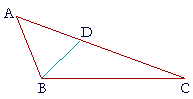
PROPOSITION 19. THEOREM

A greater angle of a triangle is opposite a greater side.

Let ABC be a triangle in which angle ABC is greater than angle BCA; then side AC is also greater than side AB.


For if it is not greater, then AC is either equal to AB or less.

But AC is not equal to AB, because

angle ABC would then equal angle ACB;	(I. 5)

but it does not;	(Hypothesis)

therefore AC is not equal to AB.

And AC is not less than AB, because

angle ABC would then be less than angle ACB;	(I. 18)

but it is not;	(Hypothesis)

therefore AC is not less than AB.

And we have shown that AC is not equal to AB.

Therefore AC is greater than AB.

Therefore, a greater angle etc. Q.E.D.

The proof involves a tacit assumption which these days is called the Law of Trichotomy. Given two magnitudes of the same kind, the first must be either equal to, less than, or greater than the second.

Trichotomy thus provides a method for indirect proof.

Please "turn" the page and do some Problems.

Continue on to the next proposition.

Previous proposition

Table of Contents | Introduction | Home

Please make a donation to keep TheMathPage online.
Even $1 will help.

Questions or comments?

E-mail: themathpage@nyc.rr.com