Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

CONSTRUCTION
OF STRAIGHT LINES
Book I. Propositions 2 and 3
AFTER STATING THE FIRST PRINCIPLES, we began with the construction of an equilateral triangle. The goal of Euclid's First Book is to prove the remarkable theorem of Pythagoras -- about the squares that are constructed of the sides of a right triangle. We will come to it.
Straightedge and compass
The object of this science is knowledge of figures, and our knowledge consists first in being able to draw the figure. Hence, the Postulates and the early propositions are devoted to what we are able to draw. Yet we draw nothing but straight lines and circles! Therefore, the only figures we can say we know will be those that we can draw with straightedge and compass.
We use a straight edge to draw a straight line. A straightedge is not a ruler, it is not used for measurement. It is the compass that becomes the measuring instrument, because with it we can make equal distances.
Use of the straightedge and compass is laid down in the first three Postulates. They are quite explicit -- and quite strict:
1. To draw a straight line from any point to any point.
2. To extend a straight line for as far as we please in a straight line.
3. To draw a circle whose center is the extremity of any straight line,
3. and whose radius is the straight line itself.
Consider now the following problem: At the point A, how may
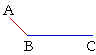
we draw a straight line equal the straight line BC? How do the postulates permit it? Logically, what are the steps?
You might think that all we do is to adjust the compass to BC and then move it over to A. But there is nothing in the Postulates that allows a compass-carried distance. Postulate 3 means that, to draw a circle, there must already be a straight line to serve as its radius. But at the point A there is no such straight line.
Hence, the duplication of BC at A is a bit challenging.
In practice, of course, we do simply adjust the compass to BC and then move it over to A. We can say, then, that the following proposition logically allows for a compass-carried distance.
Here is the formal proof. As always, to avoid scrolling, the figure will be repeated.
PROPOSITION 2. PROBLEM
| 1. | From a given point to draw a straight line equal to a given straight line. | |||
| 2. | Let A be the given point, and BC the given straight line; | |||
| 3. | we are required to draw from the point A a straight line equal | |||
| 4. | to BC. | |||
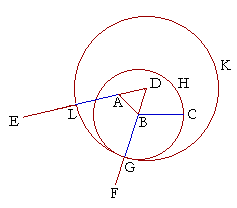 |
||||
| (The construction begins by drawing the equilateral triangle ABD; then extending DA, DB, to E and F; drawing a circle with radius BC, thus making BG equal to BC; then making DG, DL radii of a circle, so that on subtracting DB, DA respectively, AL will equal BG and therefore BC.) |
||||
| 5. | From the point A to the point B, draw the straight line AB; | |||
| (Postulate 3) | ||||
| 6. | and on it draw the equilateral triangle ABD; | (I. 1) | |||
| 7. | and extend the straight lines DA, DB to E, F. | (Postulate 2) | |||
| 8. | With B as center and BC as radius, draw the circle CHG, | ||||
| 9. | meeting DF at G. | (Postulate 3) | |||
| 10. | With D as center and DG as radius, draw the circle GKL, | ||||
| 11. | meeting DE at L. | (Postulate 3) | |||
| 12. | Then AL will equal BC. | ||||

| 13. | For, since B is the center of the circle CHG, | ||||
| 14. | BC is equal to BG. | (Definition 15) | |||
| 15. | And since D is the center of circle GKL, | ||||
| 16. | DL is equal to DG. | ||||
| 17. | But in those lines, DA is equal to DB; | (Definition 8) | |||
| 18. | therefore the remainder AL is equal to the remainder BG. | ||||
| (Axiom 3) | |||||
| 19. | And we have shown that BC is equal to BG; | ||||
| 20. | therefore each of the straight lines AL, BC is equal to BG. | ||||
| 21. | And things equal to the same thing are equal to one another. | ||||
| (Axiom 1) | |||||
| 22. | Therefore AL is equal to BC. | ||||
| 23. | Therefore from the given point A we have drawn a straight line | ||||
| 24. | AL equal to the straight line BC. | ||||
| 25. | Which is what we wanted to do. | ||||
![]()
This proposition leads directly to the next one, where we will be required to cut off from the longer of two straight lines a length equal to the shorter line. The solution is obvious -- but notice how we must rely on Proposition 2; line 6 below.
The student should now begin to see how each proposition depends on previous propositions. That is the nature of any logical theory. That is the axiomatic method.
PROPOSITION 3. PROBLEM
| 1. | Given two unequal straight lines, to cut off from the longer line | |
| 2. | a straight line equal to the shorter line. | |
| 3. | Let AB and C be the two given straight lines, and let AB be | |
| 4. | longer; | |
| 5. | we are required to cut off from AB a straight line equal to C. | |
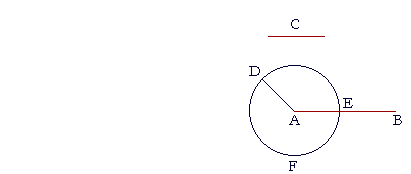 |
||
| 6. | From the point A draw AD equal to C; | (Proposition 2) |
| 7. | and with A as center and radius AD, draw the circle DEF. | |
| (Postulate 3) | ||
| 8. | Then, since the point A is the center of circle DEF, | |
| 9. | AE is equal to AD. | (Definition 15) |
| 10. | But C is also equal to AD. | (Construction) |
| 11. | Therefore each of the lines AE, C is equal to AD. | |
| 12. | Therefore AE is equal to C. | (Axiom 1) |
| 13. | Therefore from AB the longer of two straight lines | |
| 14. | we have cut off a straight line AE equal to C, the shorter line. | |
| 15. | Which is what we wanted to do. | |
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2006-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com