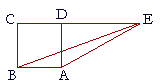
Book I.  Proposition 46

Problems

1.   State the defintion of a square.

A square is a quadrilateral in which all the sides are equal, and all the angles are right angles.

2.   a)  In Proposition 46, what is given?

A straight line.

2.  b)  What are we asked to do?

To draw a straight line on it.

2.  c)  Practice Proposition 46.

3.   Prove:  If a parallelogram has one right angle, then all its angles right angles.
3.   That is, it is a rectangle.

4.   ABCD is a square, and angle ADE is a right angle.  Prove that the
4.   square ABCD is double triangle ABE.

First, DE is in a straight line with CD.  (I. 14)
The conclusion then follows from I. 41.

5.   a)  Prove:  Squares drawn on equal straight lines are equal to one another.

5.   b)  State and prove the converse.

Here is the converse:
If two squares are equal, then the straight lines on which they are drawn are equal.

Next proposition

Previous proposition

Table of Contents | Introduction | Home

---

Please make a donation to keep TheMathPage online.
Even $1 will help.

---

Copyright © 2006-2007 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com