Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

CONSTRUCTION OF A SQUARE
Book I. Proposition 46
WE ARE JUST ABOUT READY to prove the Pythagorean theorem, which is about the squares that are drawn on the sides of a right-angled triangle. The following proposition will show that the figure we construct satisfies the definition of a square, and therefore that the figure we have called a "square" actually exists.
PROPOSITION 46. PROBLEM
| On a given straight line to draw a square. | |
| Let AB be the given straight line; we are required to draw a square on AB. |
|
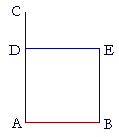 |
|
| From the point A draw AC at right angles to the straight line AB, | (I. 11) |
| and make AD equal to AB; | (I. 3) |
| through the point D draw DE parallel to AB; | (I. 31) |
| and through the point B draw BE parallel to AD. | |
| Then ADEB is a square. | |
| For, ADEB is by construction a parallelogram; | (Definition 14) |
| therefore AB is equal to DE, and AD is equal to BE. | (I. 34) |
| But AB is equal to AD. | (Construction) |
| Therefore the four straight lines AD, DE, EB, BA are equal to one another, so that the parallelogram ADEB is equilateral. |
(Axiom 1) |
| Next, all its angles are right angles. | |
 |
|
| For, since the straight line AD meets the parallel lines DE, AB, it makes angles BAD, ADE equal to two right angles. |
(I. 29) |
| But angle BAD is a right angle; | (Construction) |
| therefore angle ADE is also a right angle. | |
| And in a parallelogram the opposite angles are equal; | (I. 34) |
| therefore each of the opposite angles DEB, EBA is also a right angle. | |
| Therefore ADEB has all its angles right angles. | |
| And we proved that all the sides were equal. | |
| Therefore ADEB is a square, | (Definition 7) |
| and we have drawn it on the given straight line AB. Q.E.F. | |
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2006-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com