Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

PERPENDICULARS
Book I. Propositions 11 and 12
WE ARE NOW GOING TO CONSTRUCT right angles. Not only will we show our geometrical skill, but we satisfy a requirement of logic: We prove that these "right angles" that we have defined exist! For a definition is required only to be understood. We may not assume that what we have defined exists.
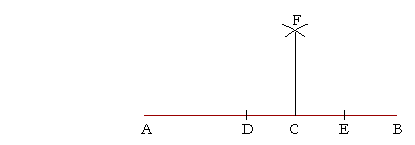
Thus, to draw a straight line at right angles to the straight line AB at the point C, place the point of the compass at C, and mark off equal distances at D and E. With D as center and radius DE, draw an arc. With E as center and with the same radius, draw an arc, and call their point of intersection F. Then CF will be perpendicular to AB at C.
Do you see why?
Here is the proof.
PROPOSITION 11. PROBLEM
| To draw a straight line at right angles to a given straight line, from a given point on it. | |
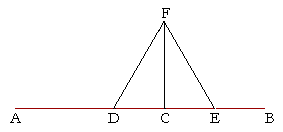
| Let AB be the given straight line, and C the given point on it; we are required to draw from the point C a straight line at right angles to the straight line AB. |
|
 |
|
| Choose any point D on AB; | |
| make CE equal to DC; | (I. 3) |
| on DE construct the equilateral triangle DFE; | (I. 1) |
| and draw CF. | |
| Then we have drawn the straight line CF at right angles to the given straight line AB, from C the given point on it. | |
| For, since DC is equal to CE, | (Construction) |
| and CF is common to triangles DCF, ECF, | |
| the two sides DC, CF are equal to the two sides EC, CF respectively; | |
| and the base DF is equal to the base EF; | (Construction) |
| therefore angle FCD is equal to angle FCE. | (S.S.S.) |
| And they are adjacent angles. | |
| And when a straight line that stands on another straight line makes the | |
| adjacent angles equal, each of those angles is a right angle; | (Definition 3) |
| therefore each of the angles FCD, FCE is a right angle. | |
| Therefore we have drawn CF at right angles to the given straight line AB, from C the given point on it. Q.E.F. | |
![]()
Using reductio ad absurdam we can prove:
Only one line can be drawn perpendicular to a given straight line
from a given point on it.
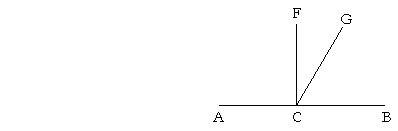
For if we suppose that CF and CG are both perpendicular to AB, then angle ACF is equal to angle ACG (Postulate 4),
the smaller to the larger; which is absurd.
Dropping a perpendicular
Here is the problem of "dropping" a perpendicular:
To a given straight line that may be made as long as we please,
and from a given point not on it, to draw a perpendicular line.

Can you solve this problem? Can you draw a perpendicular line from C to AB?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
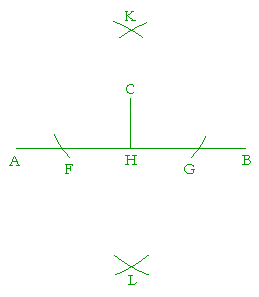
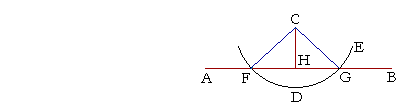
Place the point of the compass at C, and with a radius greater than the distance of C to AB, draw arcs at F and G. Now bisect the straight line FG at H. That is, with F as center and radius FG, draw arcs. With G as center and that same radius, draw arcs intersecting those at K and L. Then the straight line KCHL will be the perpendicular bisector of FG.
Why?
Here is the proof.
PROPOSITION 12. PROBLEM