Proof of the sum formulas

Theorem.		sin ( + β)	=	sin cos β + cos sin β
and
		cos ( + β)	=	cos cos β − sin sin β.

Proof.   Let the straight line AB revolve to the point C and sweep out the

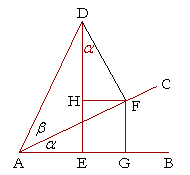
angle , and let it continue to D and sweep out the angle β;

draw DE perpendicular to AB.

Then we are to determine sin ( + β), which is

ED DA

,

and cos ( + β), which is

AE DA

.

Draw DF perpendicular to AC,

draw FG perpendicular to AB,

and draw FH perpendicular to ED.

Then angle HDF is equal to angle .

For, since the straight line AC crosses the parallel lines HF, AB, it makes the alternate angles equal (Theorem 8);

therefore angle HFA is equal to angle .

And by the construction, angle DFH is the complement of angle HFA;

therefore angle HDF (the complement of DFH) is also equal to angle .

Now,

	ED = GF + HD.
Therefore, on dividing by DA,
sin ( + β)  =	ED DA	=	GF DA	+	HD DA

	=	GF AF	AF DA	+	HD FD	FD DA
	=	sin cos β + cos sin β.

Next,

	EA = GA − FH.
Therefore,
cos ( + β)  =	EA AD	=	GA AD	−	FH AD

	=	GA AF	AF AD	−	FH DF	DF AD
	=	cos cos β − sin sin β.

This is what we wanted to prove.

The difference formulas can be proved from the sum formulas, by replacing +β with +(−β), and using these identities:

cos (−β) = cos β 

sin (−β) = −sin β.

Topic 17

Back to Trigonometric identities

Table of Contents | Home

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2001-2007 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com