This means that, in calculation, we may replace either member of the identity with the other.
We use an identity to give an expression a more convenient form. In calculus and all its applications, the trigonometric identities are of central importance.
On this page, we will present the main identities. The student will have no better way of practicing algebra than by proving them. Links to the proofs appear below.
Pythagorean identities
| a) |
sin²θ + cos²θ |
= |
1 |
| |
| b) |
1 + tan²θ |
= |
sec²θ |
| |
| c) |
1 + cot²θ |
= |
csc ²θ |
a') sin²θ = 1 − cos²θ. cos²θ = 1 − sin²θ.
These are called Pythagorean identities, because, as we will see in their proof, they are the trigonometric version of the Pythagorean theorem.
The two identities labeled a') -- "a-prime" -- are simply different versions of a). The first shows how sin θ may be expressed in terms of cos θ; the second shows how cos θ may be expressed in terms of sin θ.
Note: sin²θ -- "sine squared theta" -- means (sin θ)².
Sum and difference formulas
sin (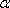 + β) + β) |
= |
sin 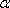 cos β + cos cos β + cos 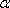 sin β sin β |
| |
sin (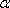 − β) − β) | = |
sin 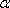 cos β − cos cos β − cos 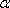 sin β sin β |
| |
cos (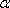 + β) + β) | = |
cos 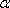 cos β − sin cos β − sin 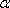 sin β sin β |
| |
cos (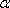 − β) − β) | = |
cos 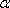 cos β + sin cos β + sin 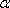 sin β sin β |
Note: In the sine formulas, + or − on the left is also + or − on the right. But in the cosine formulas, + on the left becomes − on the right; and vice-versa.
Since these identities are proved directly from geometry, the student is not normally required to master the proof. However, all the identities that follow are based on these sum and difference formulas. The student should definitely know them.
To see the proof of the sum formulas, click here.
Sums as products
| e) |
sin A + sin B
| = |
2 sin ½ (A + B) cos ½ (A − B) |
| |
| f) |
sin A − sin B
| = |
2 sin ½ (A − B) cos ½ (A + B) |
| |
| g) |
cos A + cos B
| = |
2 cos ½ (A + B) cos ½ (A − B) |
| |
| h) |
cos A − cos B
| = |
−2 sin ½ (A + B) sin ½ (A − B) |
In the proofs, the student will see that the identities e) through h) are inversions of a) through d) respectively, which are proved first. In calculus, the identity f) is used to prove one of the main theorems, namely, the derivative of sin x.
The student should not attempt to memorize these identities. Practicing their proofs -- and seeing that they come from the sum and difference formulas -- is enough.
The Topics | Home
www.proyectosalonhogar.com