Some Theorems of Plane Geometry

HERE ARE THE FEW THEOREMS that every student of trigonometry should know.

To begin with, a theorem is a statement that can be proved. We shall not prove the theorems here, however. (Those from Euclid's First Book are proved here.) Rather, we will present each one with its enunciation and its specification. The enunciation states the theorem in general terms. The specification restates the theorem with respect to a specific figure. (See Theorem 1 below.)

First, though, here are some basic definitions.

11. An angle is the inclination to one another of two straight lines that meet.

12. The point at which two lines meet is called the vertex of the angle; plural, vertices.

13. If a straight line that stands on another straight line makes the adjacent angles equal, then each of those angles is called a right angle; and the straight line that stands on the other is called a perpendicular to it.

14. An acute angle is less than a right angle. An obtuse angle is greater than a right angle.

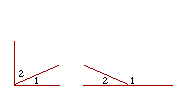
15. Angles are complementary (or complements of one another) if, together, they equal a right angle. Angles are supplementary (or supplements of one another) if together they equal two right angles.

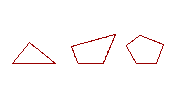
16. Rectilinear figures are figures bounded by straight lines. A triangle is bounded by three straight lines, a quadrilateral by four, and a polygon by more than four straight lines.

17. A regular polygon has equal sides and equal angles.

18. An equilateral triangle has three equal sides. An isosceles triangle has two equal sides. A scalene (or oblique) triangle has three unequal sides.

19. The vertex angle of a triangle is the angle opposite the base.

10. The height of a triangle is the straight line drawn from the vertex perpendicular to the base.

11. A right triangle is a triangle that has a right angle.

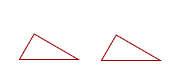
12. Figures are congruent when, if one of them were placed on the other, they would exactly coincide. (Congruent figures are thus equal to one another in all respects.)

13. Parallel lines are straight lines that are in the same plane and do not meet, no matter how far extended in either direction.

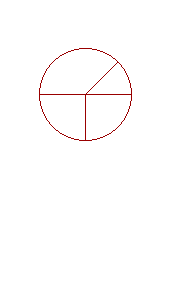
14. A circle is a plane figure bounded by one line, called the circumference, such that all straight lines drawn from a certain point within the figure to the circumference, are equal to one another.

15. And that point is called the center of the circle.

16. A straight line from the center to the circumference is a called a radius. A diameter of a circle is a straight line through the center and terminating in both directions on the circumference.

17. A chord of a circle is a straight line that joins any two points on the circumference.

18. A secant is a straight line that cuts a circle.

19. A tangent is a straight line that touches a circle but does not cut it, however it may be extended.

20. A central angle has its vertex at the center of the circle.

Here is our first theorem. It asserts a condition for triangles to be congruent. The enunciation appears in italics. The specification follows.

Theorem 1. (Euclid, I. 4.) If two triangles have two sides equal to two sides respectively, and if the angles contained by those sides are also equal, then the triangles will be equal in all respects.

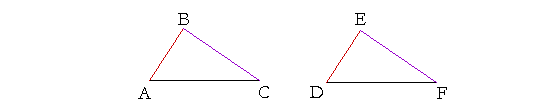
Let triangles ABC, DEF have the two sides AB, BC equal to the two sides DE, EF respectively;

and let angle ABC be equal to angle DEF;

then the remaining side AC will equal the remaining side DF;

the triangles themselves will be equal areas;

and the angle at A (opposite the side BC) will equal the angle at D (opposite the equal side EF), and the angle at C (opposite the side AB) will equal the angle at F (opposite the equal side DE).

The expression equal "respectively" means each one to each one. It is in distinction to "together" equal, which would mean that the sum of AB, BC is equal to the sum of DE, EF.

This theorem is known briefly as "S. A. S." (Side-Angle-Side). It is one of four sufficient conditions for triangles to be congruent. Others are "S. S. S." (Side-Side-Side. Euclid, I. 8.) and "A. S. A." (Angle-Side-Angle. Euclid, I. 26.).

A further condition, Side-Side-Angle, is known as the ambiguous-case.

Theorem 2 is a simple consequence of Theorem 1, and the student should be able to prove it easily.

Theorem 2. The straight line that bisects the vertex angle of an isosceles triangle is the perpendicular bisector of the base.

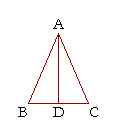
Let the straight line AD bisect the vertex angle of the isosceles triangle BAC, so that the angles BAD, DAC are equal to one another. Then AD is the perpendicular bisector of the base BC. That is, angles ADB, ADC are right angles, and the straight line BD is equal to the straight line DC.

To see the proof, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").

Triangles BAD, CAD are congruent: S.A.S. Therefore, angle ADB is equal to angle ADC, and therefore they are right angles (Def. 3). And BD equal to DC, because they are opposite the equal angles BAD, DAC. AD therefore is the perpendicular bisector of the base.

Theorem 3. (Euclid, I. 5.) In an isosceles triangle the angles at the base are equal.

Let ABC be an isosceles triangle with the equal sides AB, AC; then the angles at the base, the angles at B and C, are equal.

Theorem 4. (Euclid, I. 6.) If two angles of a triangle are equal, then the sides that subtend those angles will be equal.

With reference to the figure above, if the angles at B and C are equal, then the sides that subtend, or are opposite, those angles will be equal, namely the sides AB, AC.

(We say in geometry that a side subtends -- literally, stretches under -- an angle.)

This theorem is called the converse of the previous one. That is, when a theorem has the form "If p, then q," then the sentence p is called the hypothesis, and the sentence q is called the conclusion. Its converse has the form "If q, then p." The hypothesis and conclusion are exchanged.

Theorem 5. (Euclid, I. 13.) When a straight line that stands on another straight line makes angles, either it makes two right angles, or it makes angles that together are equal to two right angles.

Let any straight line AB stand on the straight line CD making angles ABD, ABC; then either angles ABC, ABD are two right angles, or together they are equal to two right angles.

Theorem 6. (Euclid, I. 19.) A greater angle of a triangle is opposite a greater side.

Let ABC be a triangle in which the angle at B is greater than the angle at C; then the side CA is greater than the side AB.

Theorem 7. (Euclid, I. 27.) If a straight line that meets two straight lines makes the alternate angles equal, then the two straight lines are parallel.

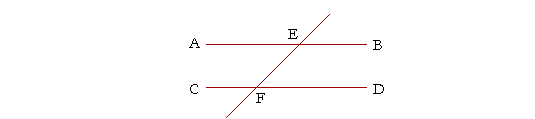
A straight line falling on two other lines.

Let the straight line EF meet the two straight lines AB, CD, and let it make the alternate angles AEF, EFD equal; then AB is parallel to CD. (For the definition of alternate angles, see Proposition I. 27 of Plane Geometry.)

Theorem 8. (Euclid, I. 29.) When a straight line crosses two parallel straight lines it makes the alternate angles equal, and it makes the exterior angle equal to the opposite interior angle on the same side.

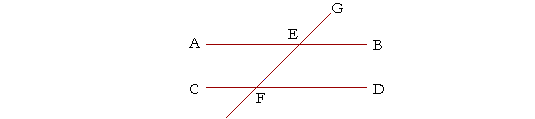
A straight line falling on two parallel lines.

If the straight lines AB, CD are parallel, and the straight line GEF crosses them, then the alternate angles AEF, EFD will be equal to one another, and the exterior angle GEA will equal the opposite interior angle, EFC.

This theorem is a partial converse of the previous one.

Theorem 9. (Euclid, I. 32.) The three angles of any triangle will equal two right angles.

Let ABC be any triangle; then the three angles at A, B, and C will together equal two right angles.

The Pythagorean proof is so simple that we will quickly show it:

Through the point A, draw a straight line PQ parallel to BC, forming the angles 1, 2, 3.

Now, angles 1, 2, 3 are together equal to two right angles. Theorem 5.

But the angle at B is equal to angle 1 -- because AB crosses the parallel lines PQ, BC, making the alternate angles equal. Theorem 8.

For the same reason, the angle at C is equal to angle 3. Therefore, the three angles A, B, C of the triangle are together equal to angles 1, 2, 3. They are equal to two right angles.

Theorem 10. (Euclid, I. 47. The theorem of Pythagoras.) In a right triangle the square drawn on the side opposite the right angle will equal the squares drawn on the sides that make the right angle.

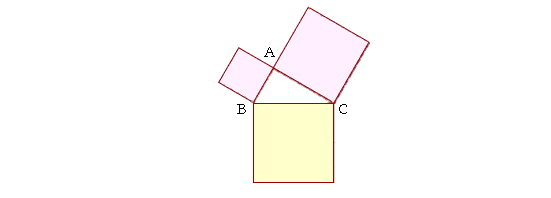
Let ABC be a right triangle in which angle CAB is a right angle; then the square drawn on BC, opposite the right angle, will equal the two squares together on CA, AB.

(For more details, see Topic 2: The Pythagorean theorem.)

Theorem 11. (Corollary to Euclid, III. 1.) The center of a circle lies on the perpendicular bisector of any chord.

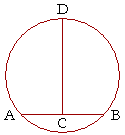
In the circle DAB let AB be any chord, and let the straight line CD be its perpendicular bisector; then the center of the circle lies on the straight line CD.

(Hence to find the center of a circle, draw two chords; draw their perpendicular bisectors; then the center of the circle will be their point of intersection.)

Theorem 12. (Euclid, III. 3.) An angle inscribed in a semi-circle is a right angle.

Let angle ABC be inscribed in the semi-circle ABC; that is, let AC be a diameter and let the vertex B lie on the circumference; then angle ABC is a right angle.

Theorem 13. (Euclid, III. 16.) The straight line drawn at right angles to a diameter of a circle from its extremity, is tangent to the circle.

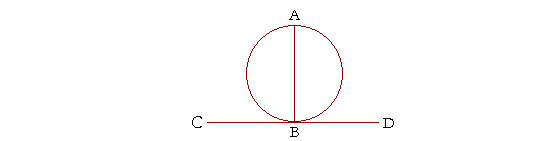
Let AB be a diameter of a circle, and let the straight line CD be drawn at right angles to AB from its extremity B; then the straight line CD is tangent to the circle.

The next theorem is its converse.

Theorem 14. (Euclid, III. 18.) If a straight line is tangent to a circle, then the radius drawn to the point of contact will be perpendicular to the tangent.

Let the straight line DE be tangent to the circle ABC at the point C; let F be the center of the circle, and draw the radius FC; then FC will be perpendicular to DE.

The following theorem shows that for triangles to be similar, it is sufficient that they be equiangular. This is basic to trigonometry. (Topic 5: Trigonometry of right triangles.)

Theorem 15. (Euclid, VI. 4.) If two triangles are equiangular, then the sides that contain the equal angles are proportional, and the sides that correspond are opposite the equal angles. Similar triangles

Let ABC, DEB be equiangular triangles with angle ABC equal to angle DEB, angle BCA equal to angle EBD, and finally angle CAB equal to angle BDE;

then in those triangles the sides that contain those equal angles are proportional,
and the side AB (opposite the angle BCA) corresponds to the side DE (opposite the equal angle EBD), and so on, for each pair of corresponding sides.

The next, and last, theorem relates arcs of circles, which are lengths, to angles. They are magnitudes of different kinds. This theorem provides among other things the basis for radian measure (Topic 14).

Theorem 16. (Euclid, VI. 33.) In the same or equal circles, arcs have the same ratio to one another as the central angles they subtend.

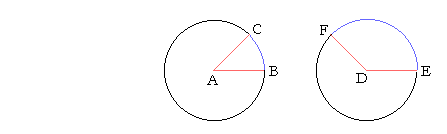
(We say in geometry that an arc "subtends" an angle; literally, stretches under.)

Let the circles with centers A and D be equal, and let angles BAC, EDF be angles at the center; then, proportionally,

Arc BC is to arc EF as angle BAC is to angle EDF.

In other words, if angle BAC is a third, say, of angle EDF, then arc BC will also be a third of arc EF.

As another example, let one "arc" be the entire circumference. Then it subtends an angle of 360°. In the same circle, let another arc subtend 60°. Then, since 60° is a sixth of of 360°, the arc that subtends 60° is a sixth of the entire circumference.

While the fact of the theorem may be obvious, the proof is quite a different matter, because it requires a satisfactory definition of "have the same ratio." Settling on such a definition was one of the great mathematical accomplishments of antiquity.

The following can be proved directly from Theorem 16:

In any circles, the same ratio of arc length to radius
determines a unique central angle that the arcs subtend.

That will provide the definiton of radian measure. We will prove that theorem in Topic 15, Arc Length.

The Topics | Home