Book I, Proposition 4Problems Back to Proposition 4. 1. What are the three magnitudes of plane geometry? To see the answer, pass your mouse over the colored area. Length, area, and angle. 2. What kind of a magnitude is a triangle? Area. 2. b) What would it mean to say that two triangles are equal? That they are equal areas. 2. c) Are equal triangles necessarily congruent? No. Triangles may be equal areas without coinciding. 2. d) Are congruent triangles necessarily equal? Yes. 3. a) State the converse of Axiom 4. Things that are equal to one another coincide with one another. 3. b) Is the converse true? No. 4. a) State the hypothesis of Proposition 4. Two triangles have two sides equal to two sides respectively, and the angles contained by those sides are also equal. 4. b) State the conclusion. The remaining side is equal to the remaining side, the triangles are equal areas, and those angles are equal that are opposite the equal sides. 5. Figure ABC is a circle with center D; ABC is a triangle with base 
Triangles ADB, ADC are congruent. For, BD is equal to DC, because they are radii of the circle. (Definition 15.) 6. In this figure, EF is equal to GH, and angle EFH is equal to angle 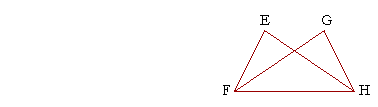
By hypothesis, EF is equal to GH, and angle EFH is equal to angle GHF. 7. ABC is a triangle, AB is equal to AC, and AE is equal to AD. Prove 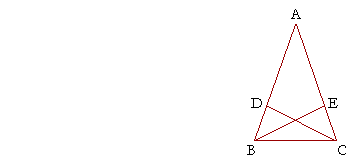
In the overlapping triangles AEB, ADC, the sides BA, AE are equal to the sides CA, AD respectively, by hypothesis. Table of Contents | Introduction | Home Please make a donation to keep TheMathPage online. Copyright © 2006-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |