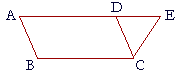
Book I.  Propositions 33 and 34

Problems

Back to Propositions 33, 34.

11.   a)  State the hypothesis of Proposition 33.

To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!

Straight lines join the extremities on the same side of two equal and parallel straight lines.

12.  b)  State the conclusion.

Those straight lines are themselves equal and parallel.

12.  c)  Practice Proposition 33.

12.   State the definition of a "parallelogram."

A parallelogram is a quadrilateral whose opposite sides are parallel.  (Definition 14)

13.   a)  State the hypothesis of Proposition 34.

A figure is a parallelogram.

13.  b)  State the conclusion.

The opposite sides and angles are equal, and the diagonal bisects the area.

13.  c)  Practice Proposition 34.

14.   The straight line ADE is parallel to the straight line BC, and AB is
14.   parallel to DC.

Prove that AB is equal to DC, and angle EDC is equal to angle DAB.

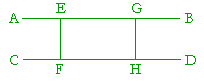
Since AD is parallel to BC, and AB is parallel to DC,
ABCD is a parallelogram.   (Definition 14)
Therefore the opposite sides AB, DC are equal.   (I. 34)
Also, because AE meets the two parallel lines AB, DC,
the exterior angle EDC is equal to the opposite interior angle DAB.   (I. 29)

15.   By the distance from a point to a line, we mean the length of the
15.   perpendicular from the point to the line.

15.   Prove that two parallel lines are everywhere the same distance apart.

Let the straight lines AB, CD be parallel, and let E and G be any two points on AB;
then the distance from E to CD is equal to the distance from G from CD.

Draw EF and GH perpendicular to CD;
then EF will be equal to GH.

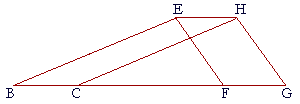
For, the straight line AB meets the two straight lines
EF, GH, and the exterior angle AEF is equal to opposite interior angle EGH,
because they are right angles;
therefore EF and GH are parallel.   (I. 28)
And by hypothesis, AB, CD are parallel.
Therefore EFHG is a parallelogram,   (Def. 14)
hence the opposite sides EF, GH are equal.   (I. 34)
And E and G were any two points on AB.
This implies that the parallel lines AB and CD are everywhere the same distance apart.

This could also be proved by showing that EG, FH are equal, and
15.  then citing I. 33.

16.   Straight lines EH, BCG are parallel; EB and HC are straight lines;
16.   BC is equal to FG; and EFGH is a parallelogram.

Prove that EBCH is a parallelogram.

Since EFGH is a parallelogram, then EH is equal to FG;   (I. 34)
but BC is equal to FG;   (Hypothesis)
therefore BC is equal to EH.   (Axiom 2)
And since EH, BC are parallel,  (Hypothesis)
and EB, HC join their extremities on the same side,
then EB, HC are parallel.   (I. 33)
Therefore EBCH is a parallelogram.   (Definition 14)

17.   Prove that a square is a certain kind of parallelogram.

18.   A rhombus is a quadrilateral which is equilateral but not
18.   right-angled.

Prove that a rhombus is a certain kind of parallelogram.

19.   A rectangle is a quadrilateral in which all the angles are right angles.

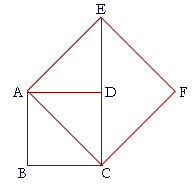
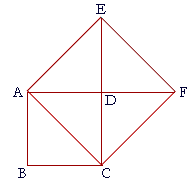
 Prove that a rectangle is a certain kind of parallelogram.

10.   ABCD is a square; ACFE is a square drawn on the diagonal
10.   AC; and ED is a straight line.

10.   a)   Prove that ED is equal to DC, and is in a straight line with DC;
10.   a)   that is, EC is the diagonal of that square.

The diagonal AC bisects ABCD into two congruent and isosceles right triangles.   (I. 34)
Since ABCD is a square, then angle BAD is a right angle;
therefore angle CAD is half a right angle.
And since CAEF is a square, angle DAE is the other half of the right angle CAE;
therefore angle DAE is equal to angle CAD.

Next, side EA is equal to side AC;
side AD is common to triangles EAD, CAD;
and we have shown that angle EAD is equal to angle CAD.
Therefore (S.A.S) the remaining side is equal to the remaining side:
ED is equal to DC;
and the remaining angles are equal:
angle EDA is equal to angle CDA.
But angle CDA is a right angle.
Therefore angle EDA is also a right angle,
and therefore ED is is a straight line with DC.   (I. 14)

10.   b)   Prove that the square drawn on the diagonal AC is twice
10.   a)   as large as the square on the side BC.

If we draw DF, then AF is also a diagonal of that square.
And each diagonal bisects that square;
therefore AF and EC divide the square into four equal and isosceles right triangles.
But the square whose side is BC is made up of two of those triangles.
Therefore the square drawn on the diagonal AC is twice the square on the side BC.
    The square drawn on the diagonal of a square is twice
the square on the side.

This theorem asserts an essential knowledge of a square figure. Moreover, it led Pythagoras to realize that the diagonal and side are incommensurable. See Topic 10 of The Evolution of the Real Numbers.

Next proposition

Previous proposition

Table of Contents | Introduction | Home

---

Please make a donation to keep TheMathPage online.
Even $1 will help.

---

Copyright © 2006-2007 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com