Equal triangles are on the same base and on the same side of it.
Those triangles are in the same parallels.
2. Proposition 40 is the partial converse of Proposition 38. State its
2. enunciation.
Equal triangles that are on equal bases and on the same side, are in the same parallels.
3. a) State the hypothesis of Proposition 41.
A parallelogram and a triangle are on same base and in the same parallels.
2. b) State the conclusion.
The parallelogram is double the triangle.
3. c) Practice Proposition 41.
4. BE is equal and parallel to CD. EA is in a straight line with DE.
9. Prove that quadrilateral EBCD is double triangle ABC.
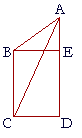
Since BE, CD are equal and parallel,
BC, ED are also equal and parallel; (I. 33)
therefore the quadrilateral EBCD is a parallelogram. (Def. 14)
And it is on the same base BC, and in the same parallels
BC, AD as triangle ABC;
therefore quadrilateral EBCD is double triangle ABC. (I. 41)
Next proposition
Previous proposition
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2006-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com