To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
Squares are drawn on each side of a right triangle.
2. a) Draw two squares. Now draw a third square equal to them.
3. ABCD is a circle with center E, and EF, EG are perpendiculars to
the
3. straight lines AB, CD respectively.
4. Proposition 48.
If the square drawn on one side of a triangle is equal to the squares
drawn on the other two sides, then the angle contained by those two sides
is a right angle.
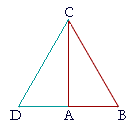
In triangle ABC, let the square drawn on BC be equal to the squares drawn on the sides CA, AB;
then angle CAB is a right angle.
From the point A, draw AD at right angles to CA;
make AD equal to BA;
and draw CD.
(The proof will now show that triangles CAD, CAB are congruent; hence angle CAB is also a right angle. The student should justify each statement.)
Then, because AD is equal to BA, the square on AD is equal to the square on BA. I-46, Problem 5a.
To each of these add the square on AC.
Therefore the squares on AD, AC are equal to the squares on BA, AC. Axiom 2

But because angle CAD is a right angle, Construction
the square on CD is equal to the squares on DA, AC. I. 47
And, by hypothesis, the square on CB is equal to the squares on BA, AC.
Therefore the square on CD is equal to the square on CB. Axiom 1
Therefore the side CD is equal to the side CB. I-46, Problem 5b.
Now, because side DA is equal to side BA,
and side CA is common to triangles CAD, CAB,
the two sides CA, AD are equal to the two sides CA, AB respectively;
and we have shown that the base CD is equal to the base CB;
therefore angle CAD is equal to angle CAB. S.S.S.
But angle CAD is a right angle; Construction
therefore angle CAB is also a right angle. Axiom 1
Therefore, if the square etc. Q.E.D.
Previous proposition
Additional exercises
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2006-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com