Vertical angles

When two straight lines AB, CD intersect one another, then angles AED, CEB are called vertical angles (or vertically opposite),

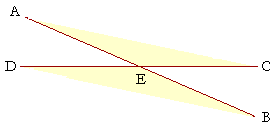
as are angles AEC, BED. Those are the two pairs of vertical angles that the intersecting straight lines form.

For, the straight angle CED -- angles CEA, AED,
is equal to the straight angle AEB -- angles BED, AED.
Therefore if we subtract angle AED from each,
then we can see that angle CEA will equal angle BED. The vertical angles are equal.

That is the next theorem.

PROPOSITION 15.  THEOREM

When two straight lines intersect one another, the vertical angles are equal.
Let the straight lines AB, CD intersect one another at the point E;
then angle AEC is equal to angle DEB,
and angle CEB is equal to angle AED.
For, since the straight line AE stands on the straight line CD,
making angles AED, AEC,
then those angles are equal to two right angles.	(I. 13)
And since the straight line DE stands on the straight line AB,
making angles AED, DEB,
then those angles also are equal to two right angles.
Therefore,
angles AED, AEC are equal to angles AED, DEB.
(Postulate 4 and Axiom 1)
From each pair, subtract angle AED.
Therefore the remaining angle AEC is equal to the remaining angle DEB.	(Axiom 3)
Similarly, we can prove that angles CEB, AED are equal.
Therefore, when two straight lines etc.  Q.E.D.