20
INVERSE TRIGONOMETRIC FUNCTIONS
UP TO NOW, we have been given an angle, and we had to evaluate a function of it. For example,
sin 30° = ½.
(Topic 7.) Or, upon consulting the Table:
cos 9° = .988.
But inversely, if we are given the value, which is a number, then the problem is to find the angle. For example,
What is the angle whose tangent is .268?
Upon inspecting the values in the tangent column of the Table, we would find:
The angle whose tangent is .268, is 15°.
The algebraic abbreviation for that sentence is
arctan .268 = 15°.
In other words, arctan N means:
"The angle whose tangent is the number N."
And similarly for
arcsin N,
arccos N,
arccot N,
arccsc N,
arcsec N.
Problem 1. Inspect the Table to evaluate the following.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
a) arcsin .616 = 38°.
b) arccos .407 = 66°.
c) arccot 2.605 = 21°.
Problem 2. Do not use the Table to evaluate the following.
a) arctan 1 = 45°. (Topic 6.)
b) arccos ½ = 60°. (Topic 7.)
c) arcsec ![]() = 45°.
= 45°.
d) arccot ![]() = 30°.
= 30°.
The inverse trigonometric functions
In theoretical work, however, the angles will be radian angles, and there will be restrictions on them. The student should be familiar with the notion of a function (Topic 3 of Precalculus) and an inverse function (Topic 19 of Precalculus).
Thus the inverse of the function
y = sin x
"The number y is the sine of the radian angle x"
is
y = arcsin x.
"y is the radian angle -- the arc (Topic 15) --
whose sine is the number x."
y = arcsin x is called the inverse sine function.
The inverse relations
If we put
f(x) = sin x
and
g(x) = arcsin x,
then according to the definition of inverse functions:
f(g(x)) = x and g(f(x)) = x.
sin(arcsin x) = x and arcsin(sin x) = x.
In particular,
| arcsin x | = | y | |
| implies, on taking the sine of both sides: | |||
| x | = | sin y. | |
For example,
| arcsin ½ | = | π 6 |
|||
| implies | |||||
| ½ | = | sin | π 6 |
. | |
(Topic 14.)
In general,
arcsin x = y implies x = sin y.
| Example 1. Evaluate arcsin | 2 |
-- "the angle whose sine is | 2 |
." |
| Solution. arcsin | 2 |
= | θ |
| implies | |||
2 |
= | sin θ. | |
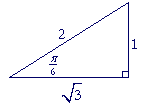
| Now, | 2 |
is the sine of what angle θ? | |
2 |
= | sin | π 4 |
(Topic 6) | |
| That is, | |||||
| arcsin | 2 |
= | π 4 |
||
| * | * | * |
Corresponding to each trigonometric function there is its inverse; namely:
| y | = | arccos x |
| y | = | arctan x |
| y | = | arccsc x |
| y | = | arcsec x |
| y | = | arccot x |
Problem 3. What does each of the following imply?
a) arccos N = θ. N = cos θ.
b) arctan t = β. t = tan β.
c) arcsec u = a. u = sec a.
| d) arccot |
π 4 |
. | = cot | π 4 |
. |
Another notation for arcsin x is sin−1x. Read: "The inverse sine of x." −1 here is not an exponent.
The range of y = arcsin x
Let us evaluate arcsin 0.
One value for the angle whose sine is 0 is 0. (Topic 16.)
But arcsin 0 = 2π, also. In fact, y could be any multiple of π!
arcsin 0 = nπ.
Therefore, so that the function y = arcsin x will be single-valued, we must restrict the values of y. We restrict them so that they will have the smallest absolute value. That will be the case when y falls within the first or fourth quadrants.
![]()
According to this restricted range, then,
If y = arcsin 0, then y = 0.
To restrict the range of arcsin x is equivalent to restricting the domain of sin x to those same values. This will be the case with all the restricted ranges that follow.
Example 2. Evaluate arcsin(−½).
Solution. arcsin(−½) = θ implies sin θ = −½.
Where is sin θ negative? In the fourth quadrant. (Topic 16.) In fact we can prove:
arcsin(−x) = −arcsin x.
See below. Therefore,
| arcsin(−½) = −arcsin ½ = − | π 6 |
. |
| * | * | * |
To see that arcsin(−x) = −arcsin x, look here:
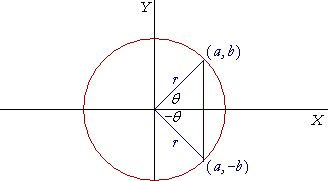
| arcsin(− | b r | ) | = | −θ |
| arcsin( | b r | ) | = | θ. |
| That is, | ||||
| arcsin(−x) | = | −arcsin x. | ||
Problem 4. Evaluate the following.
| a) arcsin 1 = | π 2 |
b) arcsin (−1) = | − | π 2 |
| c) sin−1 | 2 |
= | π 4 |
d) sin−1(− | 2 |
) = | − | π 4 |
The range of y = arctan x
Similarly, we must restrict the range of y = arctan x. Like y = arcsin x, y = arctan x has its smallest absolute values in the first and fourth quadrants.
![]()
| Note that y -- that angle whose tangent is x -- must be greater than − | π 2 |
| and less than | π 2 |
. For, the tangent is not defined at those quadrantal angles. |
(Topic 16.)
Also, like y = arcsin (−θ),
arctan (−θ) = −arctan θ.

| arctan θ | = | b a |
| arctan(−θ) | = | −b a |
| Therefore, | ||
| arctan(−θ) | = | −arctan θ. |
Problem 5. Evaluate the following.
| a) arctan 1 = | π 4 |
b) arctan (−1) = | − | π 4 |
| c) tan−1 |
= | π 3 |
d) tan−1(− |
= | − | π 3 |
| e) arctan 0 = | 0 | f) | = | − | π 6 |
The range of y = arccos x
The values of y = arccos x will have their smallest absolute values when y falls within the first or second quadrants.
![]()
Example 3. Evaluate
a) arccos ½
| Solution. The radian angle whose cosine is ½ is | π 3 |
(60°). |
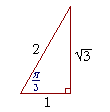
b) arccos (−½)
Solution. An angle θ whose cosine is negative falls in the 2nd quadrant.
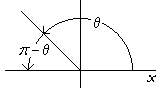
And the cosine of a 2nd quadrant angle is the negative of the cosine of its supplement. (Topic 17 of Trigonometry.) This implies:
An angle θ whose cosine is −x is the supplement
of the angle whose cosine is x.
arccos (−x) = π − arccos x.
Therefore,
| arccos (−½) | = | π − arccos ½ |
| = | ||
| = | 2π 3 |
Problem 6. Evaluate the following.
| a) arccos 1 = | 0 | b) arccos (−1) = | π |
| c) cos−1 | 2 |
= | π 4 |
d) cos−1(− | 2 |
) = | 3π 4 |
| e) arccos 0 = | π 2 |
f) | 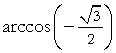 |
= | 5π 6 |
The range of y = arcsec x
In calculus, sin−1x, tan−1x, and cos−1x are the most important inverse trigonometric functions. Here, nevertheless, are the ranges that make the rest single-valued.
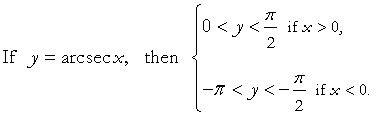
Similarly for y = arccsc x.
![]()
Next Topic: Trigonometric identities
www.proyectosalonhogar.com