Introducción al
Álgebra - Lo Básico
El Álgebra es
muy divertida – ¡puedes resolver acertijos con ella!
Un Acertijo
¿Cuál es el número que falta?
Bueno pues, la respuesta es 6,
¿no? Porque 6-2=4.
Bien, en Álgebra no usamos
espacios vacíos o cajas sino que usamos una letra (normalmente
una x o una y, pero cualquier letra está bien). Entonces
escribiríamos:
Es así de sencillo. La letra
(en este caso una x) sólo quiere decir “aún no lo sabemos” y se
la llama frecuentemente incógnita o variable.
Y una vez que la resuelves,
escribes:
¿Por qué usar una letra?
| |
Porque: |
 |
es más fácil escribir
“x” que dibujar cajitas vacías (y más fácil decir “x”
que “caja vacía”) |
 |
si hubiera muchas
cajitas vacías (muchas “incógnitas”) podríamos utilizar
una letra diferente para cada una. |
Cómo Resolver
El álgebra es como un acertijo
donde empiezas con algo como “x-2=4” y quieres llegar a algo
como “x=6”.
Pero en lugar de decir
“obviamente x=6”, usa el siguiente método paso a paso:
- Piensa qué es lo que
debes quitar para llegar a “x=…”
- Quítalo haciendo lo
opuesto (sumar es opuesto a restar)
- Esto último hazlo en
ambos lados
Aquí tienes un ejemplo:
| Queremos quitar el
“-2” |
Para quitarlo,
haz lo opuesto, en este caso suma 2 |
Hazlo en ambos
lados: |
Lo cual es ... |
¡Resuelto! |
 |
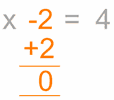 |
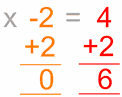 |
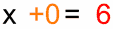 |
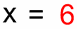 |
¿Por qué agregamos 2 a ambos
lados?
Para “mantener el equilibrio”…
| |
Agrega 2 a la
izquierda |
Agrega 2 a la derecha también |
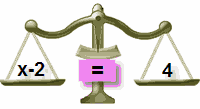 |
 |
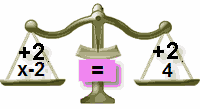 |
|
Equilibrada |
¡Desequilibrada! |
Equilibrada de nuevo |
Acuérdate de esto:
Para mantener el
equilibrio, ¡lo que se hace a un lado del “=”
también debe hacerse al otro lado! |
Otro Acertijo
Resuelve éste:
|
Comienza con: |
x + 5 = 12 |
| |
| Lo que
estás buscando es una respuesta como “x=…” ¡y el +5
está molestando!
Si restas 5, puedes
cancelar el +5 (porque 5-5=0) |
|
| |
|
|
Entonces, intentemos restar 5 en ambos lados: |
x+5 -5 = 12
-5 |
| |
|
| Un
poquito de aritmética (5-5=0 y 12-5=7) da como
resultado: |
x+0 = 7 |
| |
|
| Lo
cual es simplemente: |
x = 7 |
| |
¡Resuelto! |
|
(chequeo rápido: 7+5=12) |
|
Inténtalo Tú Mismo
Ahora practica con estos
Ejercicios Simples de Álgebra:
Resuelve los
siguientes problemas
Solución al
final de la página
Intenta utilizar los pasos que
te hemos mostrado aquí, en lugar de adivinar
El orden de las
operaciones
Operaciones
Las
"operaciones" son por ejemplo sumar,
restar, multiplicar, dividir, calcular el
cuadrado, etc. Si algo no es un número entonces
probablemente es una operación.
Pero, cuando ves algo como...
7 + (6 × 52
+ 3)
... qué parte tendrías que calcular primero?
¿Empiezas por la izquierda y vas hacia la
derecha?
¿O de derecha a izquierda?
Atención: ¡Si lo calculas en el orden
equivocado, tendrás una respuesta equivocada!
Así que hace
tiempo la gente se puso de acuerdo en seguir
algunas reglas para hacer cálculos, y son:
El orden de
las operaciones
Primero haz
las cosas entre paréntesis. Ejemplo:
 |
|
6 × (5 +
3) |
= |
6 ×
8 |
= |
48
|
|
 |
|
6 × (5 +
3) |
= |
30 + 3 |
= |
33
|
(mal) |
Exponentes
(potencias, raíces) antes que multiplicaciones,
divisiones, adiciones o sustracciones.
Ejemplo:
 |
|
5 × 22 |
= |
5 ×
4 |
= |
20
|
|
 |
|
5 × 22 |
= |
102 |
= |
100
|
(mal) |
Multiplicar
o dividir va antes que sumar o restar.
Ejemplo:
 |
|
2 + 5 × 3
|
= |
2 +
15 |
= |
17
|
|
 |
|
2 + 5 × 3
|
= |
7 × 3 |
= |
21
|
(mal) |
Aparte de
eso se va de izquierda a derecha. Ejemplo:
 |
|
30 ÷ 5 × 3
|
= |
6 × 3 |
= |
18
|
|
 |
|
30 ÷ 5 × 3
|
= |
30 ÷
15 |
= |
2
|
(mal) |
¿Cómo me puedo
acordar? ¡PEMDAS!
|
|
|
|
P
|
Paréntesis
primero |
|
E
|
Exponentes
(potencias y raíces cuadradas, etc.) |
|
MD
|
Multiplicación
y División (de izquierda a
derecha) |
|
AS
|
Adición
y Sustracción (de izquierda a
derecha) |
|
Nota:
multiplicar y dividir están al mismo
nivel. Sumar y restar están al
mismo nivel. |
 |
|
Después de
hacer "P" y "E", sólo ve de izquierda a
derecha haciendo las "M" o
"D" cuando te encuentres una.
Entonces ve de izquierda a derecha
haciendo las "A" o "S"
cuando las encuentres. |
Nota: no
hace falta que te aprendas PEMDAS si no quieres,
lo importante es que te aprendas el orden de las
operaciones correctamente.
Ejemplos
Ejemplo: ¿Cómo
calculas 3 + 6 × 2 ?
Multiplicación
antes que Adición:
Primero
6 × 2 = 12, después 3 + 12 = 15
Ejemplo: ¿Cómo
calculas (3 + 6) × 2 ?
Paréntesis
primero:
Primero
(3 + 6) = 9, después 9 × 2 = 18
Ejemplo: ¿Cómo
calculas 12 / 6 × 3 ?
Multiplicación
y División están al mismo nivel, ve
de izquierda a derecha:
Primero
12 / 6 = 2, después 2 × 3 = 6
Ah, sí, ¿y qué
pasa con 7 + (6 × 52 + 3)?
|
7 + (6 × 52
+ 3) |
|
|
7 + (6 ×
25 + 3) |
Empieza
dentro del paréntesis, y después
haz los exponentes primero |
|
7 + (150 +
3) |
Después
multiplica |
|
7 + (153) |
Después
suma |
|
7 + 153 |
Paréntesis hecho, la última
operación es una suma |
|
160 |
¡HECHO! |
|
|
Álgebra -
Sustituciones
"Sustituir" significa poner algo en lugar de
otra cosa.
Sustitución
En álgebra
"sustitución" significa poner números donde hay
letras:
 |
Si
tienes: |
|
 |
Y
sabes que x=6 ... |
|
 |
...
entonces puedes "sustituir" 6
por x: |
|
Ejemplo 1: si x=5 y y=3, ¿cuánto es
10/x + 2y ?
Pon "5" donde
esté la "x", y "3" donde esté la "y":
10/5 + 2×3 = 2 + 6 = 8
Ejemplo 2: Si x=3 y y=4, ¿cuánto es x2
+ xy ?
Pon "3" donde
esté la "x", y "4" donde esté la "y": 32
+ 3×4 = 9 + 12 = 21
Ejemplo 3: Si x=3 (pero no conoces "y"),
¿cuánto es x2 + xy ?
Pon "3" donde
esté la "x": 32 + 3y = 9 + 3y
(esto es todo lo que puedes hacer)
Y como muestra
este último ejemplo, no siempre tendrás un
número como respuesta, a veces sólo una fórmula
más simple. |
|
Ecuaciones y
fórmulas
Qué es una
ecuación
Una ecuación
dice que dos cosas son iguales. Tendrá un signo
de igualdad "=", por ejemplo:
Lo que la
ecuación dice: lo que está a la izquierda (x
+ 2) es igual que lo que está en la derecha (6)
Así que una
ecuación es como una afirmación "esto
es igual a aquello"
Qué es una
fórmula
Una fórmula es
un tipo especial de ecuación que muestra la
relación entre diferentes variables (una
variable es un símbolo que representa un número
que no conocemos todavía).
Ejemplo: La
fórmula para calcular el volumen de una caja
es
V = lpa
V significa
volumen, l longitud, p profundidad y a
altura.
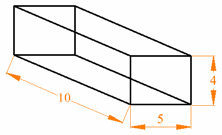 Si l=5, p=10 y a=4, entonces V = 5×10×4 =
200
Si l=5, p=10 y a=4, entonces V = 5×10×4 =
200
Una fórmula
tiene más de una variable.
Todas estas son
ecuaciones, pero sólo algunas son fórmulas:
|
x
= 2y - 7 |
Fórmula (que relaciona x e
y) |
|
a2
+ b2 = c2 |
Fórmula (que relaciona a,
b y c) |
|
x/2
+ 7 = 0 |
No
es una fórmula (sólo una ecuación) |
Sin el igual
A veces una
fórmula se escribe sin el "=":
Ejemplo: la
fórmula para el volumen de una caja es:
lpa
Pero de alguna
manera el "=" está allí, porque podrías haber
escrito V = lpa si hubieras querido.
Sujeto de una
fórmula
El "sujeto" de
una fórula es la variable sola (normalmente a la
izquierda del "=") que es igual a todo lo demás.
Ejemplo: en la
fórmula
s = vt + ½ at2
"s" es el sujeto
de la fórmula
Cambiar el
sujeto
Una de las
cosas más poderosas que puede hacer el Álgebra
es "transformar" una fórmula para que otra
variable sea el sujeto.
Transformar la
fórmula del volumen de una caja (V = lpa)
para que la longitud sea el sujeto:
|
EMpieza por: |
V = lpa |
|
divide los dos lados entre p: |
V / p = la |
|
divide los dos lados entre a: |
V / pa = l |
|
intercambia los lados: |
l = V / pa |
Así que si
tienes una caja con profundidad 2m, altura
2m y volumen 12m3, puedes
calcular su longitud:
l = V / pa
l = 12m3
/ (2m×2m) = 12/4 = 3m
|
|
Álgebra -
Definiciones básicas
Qué es una
ecuación
Una ecuación
dice que dos cosas son iguales. Tendrá un signo
de igualdad "=", por ejemplo:
Lo que esta
ecuación dice: lo que está a la izquierda (x
+ 2) es igual que lo que está en la derecha (6)
Así que una
ecuación es como una afirmación "esto
es igual a aquello"
Partes de una
ecuación
Para que la
gente pueda hablar de ecuaciones, hay nombres
para las diferentes partes (¡mejor que decir
"esta cosa de aquí"!)
Aquí tienes una
ecuación que dice 4x-7
es igual a 5, y todas
sus partes:
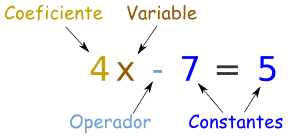 |
Una
variable es un símbolo para un
número que todavía no conocemos.
Normalmente es una letra como x o y.
Un número
solo se llama una constante.
Un
coeficiente es un número que está
multiplicando a una variable (4x
significa 4 por x, así que 4 es un
coeficiente)
Un
operador es un símbolo (como +, ×,
etc) que representa una operación (es
decir, algo que quieres hacer con los
valores). |
|
|
|
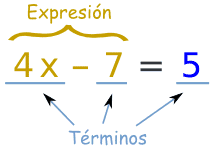 |
Un
término es o bien un número o
variable solo, o números y variables
multiplicados juntos.
Una
expresión es un grupo de términos
(los términos están separados por signos
+ o -) |
Ahora podemos
decir cosas como "esa expresión sólo tiene dos
términos", o "el segundo término es constante",
o incluso "¿estás seguro de que el coeficiente
es 4?"
¡Exponente!
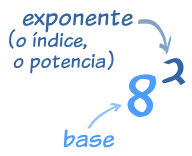 |
El
exponente (como el 2 en x2)
dice cuántas veces usar el valor
en una multiplicación.
Ejemplos:
82
= 8 × 8 = 64
y3
= y × y × y
y2z
= y × y × z
|
Los exponentes
hacen más fácil escribir y usar muchas
multiplicaciones
Ejemplo: y4z2
es más fácil que y × y × y × y × z × z,
o incluso yyyyzz
Polinomio
Un ejemplo de
un polinomio: 3x2 + x - 2
Un polinomio
puede tener constantes, variables
y los exponentes 0,1,2,3,...
Y se puede
combinar haciendo sumas, restas y
multiplicaciones... ¡pero no divisiones!
Monomio,
binomio, trinomio
Hay nombres
especiales para polinomios con 1, 2 o 3
términos:
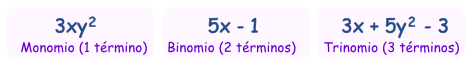
Términos similares
"Términos
similares" son términos cuyas variables
(y sus exponentes como el 2 en x2)
son los mismos.
En otras
palabras, términos que "se parecen". (Nota: los
coeficientes pueden ser distintos)
Ejemplos:
|
Términos |
Por qué son "similares" |
 |
7x |
x |
-2x |
porque las variables son todas x |
 |
(1/3)xy2 |
-2xy2 |
6xy2 |
porque las variables son todas xy2 |
Puedes
sumar los términos similares para
hacer un solo término:
Ejemplo: 7x
+ x = 8x
Términos
no similares
Si no son
términos similares, simplemente se les llama
"términos no similares":
|
Términos |
Por qué no son "similares" |
 |
-3xy |
-3y |
12y2 |
← estos
son términos no similares
(xy, y e y2
son todos diferentes) |
Solución:
|
1: |
|
x+9 = 11 |
|
|
| |
|
Comienza con:
|
x+9 = 11 |
|
Resta 9 de ambos
lados:
|
x = 2 |
|
|
|
2: |
|
x-10 = 0 |
|
|
| |
|
Comienza con:
|
x-10 = 0 |
|
Suma 10 a ambos
lados:
|
x = 10 |
|
|
|
3: |
|
x+7 = 17 |
|
|
| |
|
Comienza con:
|
x+7 = 17 |
|
Resta 7 de ambos
lados:
|
x = 10 |
|
|
|
4: |
|
2+x = 8 |
|
|
| |
|
Comienza con:
|
2+x = 8 |
|
Resta 2 de ambos
lados:
|
x = 6 |
|
|
|
5: |
|
9+x = 16 |
|
|
| |
|
Comienza con:
|
9+x = 16 |
|
Resta 9 de ambos
lados:
|
x = 7 |
|
|
|
6: |
|
x+5 = 13 |
|
|
| |
|
Comienza con:
|
x+5 = 13 |
|
Resta 5 de ambos
lados:
|
x = 8 |
|
|
|
7: |
|
-9+x = -2 |
|
|
| |
|
Comienza con:
|
-9+x = -2 |
|
Suma 9 a ambos
lados:
|
x = 7 |
|
|
|
8: |
|
x+7 = 9 |
|
|
| |
|
Comienza con:
|
x+7 = 9 |
|
Resta 7 de ambos
lados:
|
x = 2 |
|
|
|
9: |
|
x-9 = -7 |
|
|
| |
|
Comienza con:
|
x-9 = -7 |
|
Suma 9 a ambos
lados:
|
x = 2 |
|
|
|
10: |
|
-10+x = 0 |
|
|
| |
|
Comienza con:
|
-10+x = 0 |
|
Suma 10 a ambos
lados:
|
x = 10 |
|
|
|
|
Sigue
>>>Exponentes>>> |