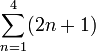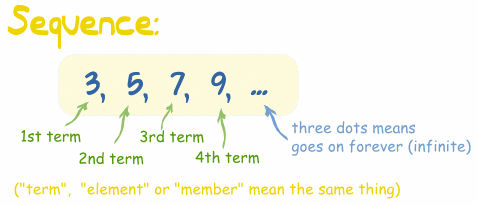|
|
Funciones, sucesiones y series, numeros irracionales y
más...
Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
Entrar a exámenes
de:
Contenido Revisado 
|
|
Notación
Para que sea más fácil
escribir las reglas, normalmente lo hacemos así:
|
|
Posición
del término
|
 |
Es normal usar
xn para los términos:
-
xn
es el término
-
n
es la posición de ese término
|
|
|
Así que para hablar del
"quinto término" sólo tienes que escribir:
x5 |
Entonces podemos
escribir la regla para {3, 5, 7, 9, ...} en forma de
ecuación, así:
xn = 2n+1
Ahora, si queremos
calcular el 10º término, podemos escribir:
x10 = 2n+1
= 2×10+1 = 21
¿Puedes calcular el
50º término? ¿Y el 500º?
Ahora veamos algunas
sucesiones especiales y sus reglas:
Tipos
de sucesiones
Sucesiones aritméticas
El ejemplo que acabamos
de usar, {3,5,7,9,...}, es una sucesión aritmética (o
progresión aritmética), porque la diferencia entre un
término y el siguiente es una constante.
Ejemplos
|
1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
Esta sucesión
tiene una diferencia de 3 entre cada dos términos.
La regla es xn =
3n-2
| 3,
8, 13, 18, 23, 28, 33, 38,
... |
Esta sucesión tiene
una diferencia de 5 entre cada dos términos.
La regla es xn = 5n-2
Sucesiones geométricas
En una sucesión
geométrica cada término se calcula multiplicando el
anterior por un número fijo.
Ejemplos:
| 2,
4, 8, 16, 32, 64, 128, 256,
... |
Esta sucesión tiene un
factor 2 entre cada dos términos.
La regla es xn = 2n
| 3,
9, 27, 81, 243, 729, 2187,
... |
Esta sucesión
tiene un factor 3 entre cada dos términos.
La regla es xn =
3n
Esta sucesión tiene un
factor 0.5 (un medio) entre cada dos términos.
La regla es xn = 4 × 2-n
Sucesiones especiales
Números triangulares
| 1,
3, 6, 10, 15, 21, 28, 36, 45,
... |
Esta sucesión se genera
a partir de una pauta de puntos en un triángulo.
Añadiendo otra fila de puntos y contando el total
encontramos el siguiente número de la sucesión.
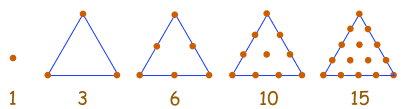
Pero es más fácil usar
la regla
xn
= n(n+1)/2
Ejemplo:
- El quinto número
triangular es x5 = 5(5+1)/2 = 15,
- y el sexto es x6
= 6(6+1)/2 = 21
Números
cuadrados
| 1,
4, 9, 16, 25, 36, 49, 64, 81,
... |
El siguiente número se
calcula elevando al cuadrado su posición.
La regla es xn
= n2
Números
cúbicos
| 1,
8, 27, 64, 125, 216, 343, 512, 729,
... |
El siguiente número se
calcula elevando al cubo su posición.
La regla es xn
= n3
Números de
Fibonacci
| 0,
1, 1, 2, 3, 5, 8, 13, 21, 34,
... |
El siguiente número se
calcula sumando los dos que están antes de él.
El 2 se calcula sumando los dos delante de él (1+1)
El 21 se calcula sumando los dos delante de él (8+13)
La regla es xn
= xn-1 + xn-2
Esta regla es
interesante porque depende de los valores de los
términos anteriores.
Por ejemplo el 6º
término se calcularía así:
x6
= x6-1 + x6-2 = x5 + x4
= 5 + 3 = 8
Series
"Sucesiones" y "series"
pueden parecer la misma cosa... pero en realidad una
serie es la suma de una sucesión.
Sucesión: {1,2,3,4}
Serie: 1+2+3+4 = 10
Las series se suelen
escribir con el símbolo Σ que
significa "súmalos todos":
 |
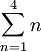Esto significa "suma de 1 a 4" = 10 |
|
|
|
|
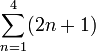
Esto significa
"suma los cuatro primeros términos de la
sucesión 2n+1"
Que son los cuatro primeros términos de nuestro
ejemplo {3,5,7,9,...} = 3+5+7+9 = 24 |
Sucesiones - Encontrar la regla
Para encontrar un número que falta en una
sucesión, primero tienes que conocer
la regla
Definición rápida de
sucesión
Lee sobre sucesiones y
series para conocer el tema bien, pero por ahora:
Una sucesión es un
conjunto de cosas (normalmente números) que están en
algún orden.
Cada número en la
sucesión es un término (a veces "elemento" o "miembro"):
Encontrar números que
faltan
Para calcular un número
que falta primero necesitas saber la regla que
sigue la sucesión.
A veces basta con mirar
los números y ver el patrón.
Ejemplo: 1, 4, 9,
16, ?
Respuesta: son
cuadrados (12=1, 22=4, 32=9,
42=16, ...)
Regla: xn
= n2
Sucesión: 1,
4, 9, 16, 25, 36, 49, ...
¿Has visto cómo
escribimos la regla con "x" y "n"?
xn
significa "el término en la posición n", así que el
tercer término sería x3
Y también hemos usado
"n" en la fórmula, así que para el tercer término
hacemos 32 = 9. Esto se puede escribir
x3 = 32
= 9
Cuando sepamos la regla,
la podemos usar para calcular cualquier término, por
ejemplo término 25º se calcula "poniendo dentro" 25
donde haya una n.
x25 = 252
= 625
Qué tal si vemos otro
ejemplo:
Ejemplo: 3, 5, 8,
13, 21, ?
Son la suma de los
dos que están delante, o sea 3 + 5 = 8, 5 + 8 = 13 y
sigue así (en realidad es parte de la Sucesión de
Fibonacci):
Regla: xn
= xn-1 + xn-2
Sucesión: 3,
5, 8, 13, 21, 34, 55, 89,
...
¿Qué significa xn-1
aquí? Bueno, sólo significa "el término anterior" porque
la posición (n-1) es uno menos que (n).
Entonces, si n
es 6, será xn = x6
(el 6º término) y xn-1 = x6-1 =
x5 (el 5º término)
Vamos a aplicar la
regla al 6º término:
x6 = x6-1 + x6-2
x6 = x5 + x4
Ya sabemos que el 4º es
13, y que el 5º es 21, así que la respuesta es:
x6 = 21 + 13 =
34
Muy simple... sólo pon
números en lugar de "n"
Muchas reglas
Uno de los problemas
que hay en "encontrar el siguiente término" de una
sucesión es que las matemáticas son tan potentes que
siempre hay más de una regla que vale.
¿Cuál es el
siguiente número de la sucesión 1, 2, 4, 7, ?
Hay (por lo menos)
tres soluciones:
Solución 1: suma 1, después suma 2, 3, 4, ...
Entonces, 1+1=2,
2+2=4, 4+3=7, 7+4=11, etc...
Regla: xn
= n(n-1)/2 + 1
Sucesión: 1,
2, 4, 7, 11, 16, 22, ...
(La regla parece
complicada, pero funciona)
Solución 2: suma los dos números anteriores más 1:
Regla: xn
= xn-1 + xn-2 + 1
Sucesión: 1,
2, 4, 7, 12, 20, 33, ...
Solución 3: suma los tres números anteriores
Regla: xn
= xn-1 + xn-2 + xn-3
Sucesión: 1,
2, 4, 7, 13, 24, 44, ...
Así que tenemos tres
soluciones razonables, y cada una da una sucesión
diferente.
¿Cuál es la correcta?
Todas son correctas.
 |
Y habrá otras
soluciones.
Hey, puede ser
una lista de números ganadores... así que el
siguiente será... ¡cualquiera! |
La regla más simple
Cuando dudes, elige
la regla más simple que funcione, pero menciona
también que hay otras soluciones.
Calcular diferencias
A veces ayuda encontrar
diferencias entre los términos... muchas veces
esto nos muestra una pauta escondida.
Aquí tienes un ejemplo
sencillo:
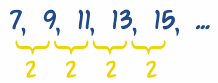
Las diferencias siempre
son 2, así que podemos adivinar que "2n" es parte de la
respuesta.
Probamos 2n:
|
n: |
1 |
2 |
3 |
4 |
5 |
|
Términos (xn): |
7 |
9 |
11 |
13 |
15 |
|
2n: |
2 |
4 |
6 |
8 |
10 |
|
Error: |
5 |
5 |
5 |
5 |
5 |
La última fila nos dice
que siempre nos faltan 5, así que sumamos 5 y acertamos:
Regla: xn = 2n
+ 5
OK, podías haber
calculado "2n+5" jugando un poco con los números, pero
queremos un sistema que funcione, para cuando las
sucesiones sean complicadas.
Segundas diferencias
En la sucesión {1,
2, 4, 7, 11, 16, 22, ...} tenemos que calcular las
diferencias...
... y después calcular
las diferencias de esas diferencias (se
llaman segundas diferencias), así:
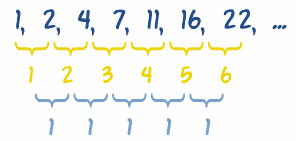
En este caso las
segundas diferencias son 1.
Con las segundas
diferencias multiplicamos por "n2 / 2".
En nuestro caso la
diferencia es 1, así que probamos n2 / 2:
|
n: |
1 |
2 |
3 |
4 |
5 |
|
Términos (xn): |
1 |
2 |
4 |
7 |
11 |
| |
|
|
|
|
|
|
n2: |
1 |
4 |
9 |
16 |
25 |
| n2
/ 2: |
0.5 |
2 |
4.5 |
8 |
12.5 |
|
Error: |
0.5 |
0 |
-0.5 |
-1 |
-1.5 |
Estamos cerca,
pero nos estamos desviando en 0.5 cada vez más, así que
probamos ahora: n2 /
2 - n/2
| n2
/ 2 - n/2: |
0 |
1 |
3 |
6 |
10 |
|
Error: |
1 |
1 |
1 |
1 |
1 |
Ahora nos sale 1 menos,
así que sumamos 1:
| n2
/ 2 - n/2 + 1: |
1 |
2 |
4 |
7 |
11 |
|
Error: |
0 |
0 |
0 |
0 |
0 |
La fórmula n2
/ 2 - n/2 + 1 se puede simplificar a
n(n-1)/2 + 1
Así que, con "prueba y
error" hemos conseguido descubrir la regla.
Sucesión: 1, 2,
4, 7, 11, 16, 22, 29, 37, ...
Otros tipos de
sucesiones
Además de las que se
explican en sucesiones y series:
- Sucesiones
aritméticas
- Sucesiones
geométricas
- Sucesión de
Fibonacci
- Sucesiones
triangulares
Ten en cuenta
- Números primos
- Números
factoriales
- ¡y cualquier otra
sucesión que veas en tus viajes!
La verdad es que hay
demasiados tipos de sucesiones para decirlos aquí, pero
si hay alguno que te gustaría que digamos, sólo tienes
que decírmelo.
Números
irracionales
Un número irracional
es un número que no se puede escribir en fracción
- el decimal sigue para siempre sin repetirse.
Ejemplo:
Pi es un número irracional. El valor de Pi
es
3.1415926535897932384626433832795 (y más...)
Los decimales no
siguen ningún patrón, y no se puede escribir
ninguna fracción que tenga el valor Pi.
Números como
22/7
= 3.1428571428571... se acercan pero no son
correctos.
 |
Se llama
irracional porque no se puede escribir en
forma de razón (o fracción),
¡no porque esté loco! |
Racional o irracional
Pero si un número se
puede escribir en forma de fracción se le llama
número racional:
Ejemplo: 9.5 se
puede escribir en forma de fracción así
19/2
= 9.5
así que no es
irracional (es un número racional)
Aquí tienes más
ejemplos:
| Números |
En
fracción |
¿Racional
o
irracional? |
|
5 |
5/1 |
Racional |
|
1.75 |
7/4 |
Racional |
| .001 |
1/1000 |
Racional |
√2
(raíz cuadrada de 2) |
? |
¡Irracional! |
Ejemplo: ¿La raíz
cuadrada de 2 es un número irracional?
Mi calculadora dice
que la raíz de 2 es
1.4142135623730950488016887242097, ¡pero eso no es
todo! De hecho sigue indefinidamente, sin que los
números se repitan.
No se puede escribir una fracción que sea
igual a la raíz de 2.
Así que la
raíz de 2 es un número
irracional
Números irracionales
famosos
 |
Pi
es un número irracional famoso. Se han calculado
más de un millón de cifras decimales y sigue sin
repetirse. Los primeros son estos:
3.1415926535897932384626433832795 (y sigue...) |
 |
El número
e (el número de Euler) es otro número
irracional famoso. Se han calculado muchas
cifras decimales de e sin
encontrar ningún patrón. Los primeros decimales
son:
2.7182818284590452353602874713527 (y sigue...) |
 |
La razón de
oro es un número irracional. Sus primeros
dígitos son:
1.61803398874989484820... (y más...) |
 |
Muchas raíces
cuadradas, cúbicas, etc. también son
irracionales. Ejemplos:
| √3 |
1.7320508075688772935274463415059
(etc) |
|
√99 |
9.9498743710661995473447982100121
(etc) |
Pero √4 = 2, y √9 = 3, así que no todas
las raíces son irracionales.
|
Historia de los
números irracionales
Aparentemente
Hipaso (un estudiante de Pitágoras)
descubrió los números irracionales intentando escribir
la raíz de 2 en forma de fracción (se cree que usando
geometría). Pero en su lugar demostró que no se puede
escribir como fracción, así que es irracional.
Pero Pitágoras no podía aceptar que
existieran números irracionales, porque creía que todos
los números tienen valores perfectos. Como no pudo
demostrar que los "números irracionales" de Hipaso
no existían, ¡tiraron a Hipaso por la borda y se ahogó!
Grado
(de una expresión)
El "grado"
se llama a veces "orden"
Grado de un polinomio
(una variable)
El grado de un
polinomio con una sola variable (como
x) es el exponente más
grande de la variable.
Ejemplos:
 |
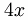El grado es
1 (una variable sin exponente tiene de hecho
exponente 1) |
|
|
|
 |
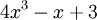El
grado es 3 (el mayor exponente de x) |
|
|
|
 |
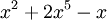El
grado es 5 (el mayor exponente de x) |
|
|
|
 |
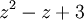El
grado es 2 (el mayor exponente de z) |
Grado de un polinomio
(más de una variable)
Si hay más de una
variable en el polinomio, tienes que mirar cada
término (los términos se separan con signos + o -):
- Calcula el grado
de cada término haciendo la suma de los
exponentes de las variables que tenga,
- El mayor de esos
grados es el grado del polinomio.
Ejemplo: cuál es
el grado de este polinomio:
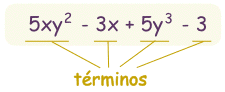
- 5xy2
tiene grado 3 (x tiene
exponente 1, y tiene 2, y 1+2=3)
- 3x
tiene grado 1 (x tiene
exponente 1)
- 5y3
tiene grado 3 (y tiene
exponente 3)
- 3
tiene grado 0 (no hay variables)
El mayor es
3, así que el polinomio tiene grado
3
Nombres de los grados
¡Cuando conoces el
grado también puedes darle un nombre!
| 0 |
constante |
| 1 |
lineal |
| 2 |
cuadrático |
| 3 |
cúbico |
| 4 |
cuártico |
| 5 |
quíntico |
Ejemplo: 5xy2
- 3 tiene grado 2, así que es cuadrático
Cuando una expresión
es una fracción
Puedes calcular el
grado de una expresión racional (una que tenga la forma
de una fracción) calculando el grado de arriba (numerador)
y restando el grado de abajo (denominador).
Aquí tienes tres
ejemplos:
Calculando otros tipos
de expresiones
Aviso: ¡Ideas
avanzadas en adelante!
A veces puedes calcular
el grado de una expresión con una división...
- el logaritmo de la
función entre
- el logaritmo de la
variable
... para
valores más y más grandes, para ver hacia donde "va" el
grado.
(Más correctamente,
deberías evaluar el límite a infinito de log(f(x))/log(x),
pero quería mantener las cosas simples).
Aquí tienes un ejemplo:
Ejemplo: ¿Cuál es el
grado de
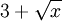(3 más la raíz cuadrada de x)?
Vamos a tomar valores
de x más y más grandes:
|
x |
log() |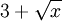
log(x) |
log()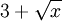
/log(x) |
|
2 |
1.48483 |
0.69315 |
2.1422 |
|
4 |
1.60944 |
1.38629 |
1.1610 |
|
10 |
1.81845 |
2.30259 |
0.7897 |
|
100 |
2.56495 |
4.60517 |
0.5570 |
|
1,000 |
3.54451 |
6.90776 |
0.5131 |
|
10,000 |
4.63473 |
9.21034 |
0.5032 |
|
100,000 |
5.76590 |
11.51293 |
0.5008 |
|
1,000,000 |
6.91075 |
13.81551 |
0.5002 |
Mirando la tabla:
- cuando x
crece log()
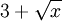/ log(x) se acerca más y más a 0.5
Así que el grado es
0.5 (o lo que es lo mismo 1/2)
(Nota: esto
coincide bien con x½ = raíz cuadrada de
x, lee exponentes fraccionarios)
Algunos valores del
grado
| Expresión |
Grado |
| log(x) |
0 |
| ex |
∞ |
| 1/x |
-1 |
 |
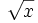1/2 |
Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
|
|
