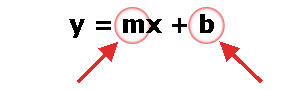Definición y áreas de interés        Proyecto Salón Hogar

 

L  a  G r a n  E n c i c l o p e d i a   I l u s t r a d a  d e l   P r o y e c t o  S a l ó n  H o g a r

 

 

Ecuación de una línea recta

>>>Introducción al Álgebra>>> >>>Ecuaciones lineales>>>
>>>Exponentes>>> >>>Ecuaciones cuadráticas>>>
>>>Simplificar>>> >>>Funciones, sucesiones y series, numeros irracionales y más...>>>
>>>Polinomios>>> >>>Funciones, sucesiones y series, numeros irracionales y más...>>>

 

Para poder tomar los exámenes

de este tema debes estar

registrado, si no lo estás,

[Registrate aquí]

Entrar a exámenes de:

Ecuación de una línea recta


La ecuación GENERAL de una línea recta tiene la forma:
 

y = mx + b

(o con otras letras, mira abajo)

¿Qué significa?

 
Ecuación de una línea recta
Gradiente Intersección Y

 

y = cuánto arriba

x = cuán lejos

m = gradiente o pendiente (cuán inclinada es la línea)

b = la intersección Y (donde la línea se cruza con el eje Y)
 

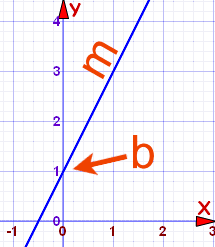
Sabiendo esto podemos encontrar la ecuación de una línea recta:

Ejemplo 1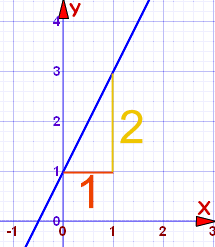



 
m  = 
2
 
1
 =  2

b = 1
 
Por lo tanto y = 2x + 1

Ejemplo 2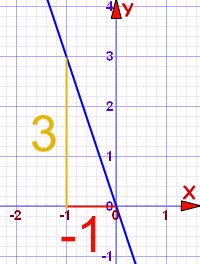

m  = 
3
 
-1
 =  –3

b = 0

Esto nos da y = –3x + 0
¡No nos hace falta poner el cero!

 
Por lo tanto y = –3x

Nota

Hay varias "notaciones" diferentes:

Aquí usamos: y = mx + b
Otra que también se usa es: y = mx + c
Y en otros sitios: y = ax + b

... pero todas significan lo mismo, sólo cambian las letras.

Coordenadas cartesianas

Las coordenadas cartesianas se pueden usar para decir dónde estás exactamente en un mapa o gráfico

Coordenadas cartesianas

Con las coordenadas cartesianas señalas un punto en un gráfico dando la distancia de lado y hacia arriba:

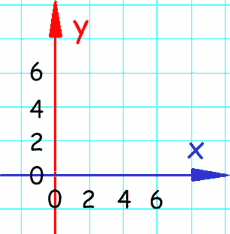
El punto (12,5) está 12 unidades a la derecha y 5 arriba.

Ejes X e Y

La dirección izquierda-derecha (horizontal) se suele llamar X ...

... y arriba-abajo (vertical) se suele llamar Y.
 

Las líneas de referencia (desde donde se miden distancias) se llaman ejes.

Hay un eje X y un eje Y.
  El eje X pasa por cero horizontalmente
El eje Y pasa por cero verticalmente

Direcciones

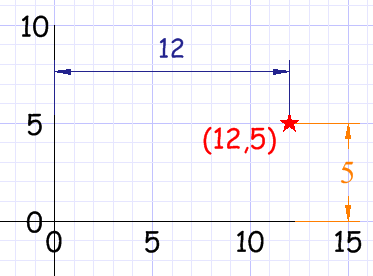
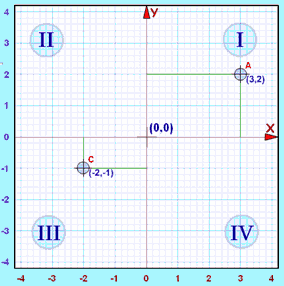
Cuando x (la primera coordenada) aumenta, el punto se mueve a la derecha. (Si disminuye, el punto va a la izquierda.)
Cuando y (la segunda coordenada) aumenta, el punto se mueve arriba. (Si disminuye, el punto va abajo.)

Escribir coordenadas

Las coordenadas siempre se escriben en el mismo orden: la dirección horizontal primero, después la vertical. Esto se llama un "par ordenado".

Y normalmente los números se separan con una coma, y se rodean con paréntesis así: (3,2)

Ejemplo: (4,9) significa 4 unidades a la derecha y 9 arriba

Ejemplo: (0,5) significa 0 unidades a la derecha y 5 arriba. En otras palabras, sólo 5 unidades arriba.

Se llaman cartesianas porque las ideó el matemático y filósofo René Descartes a quien también se llamaba Cartesio. Es famoso por la frase "Pienso, luego existo".

Cuadrantes

¿Qué pasa cuando x o y es negativo? ¡Pues que empezamos en cero y vamos en la dirección contraria!

Esto significa que es posible tener combinaciones como x positivo e y negativo, o los dos negativos. De hecho hay cuatro combinaciones, y en un gráfico se llaman cuadrantes:

X
(horizontal)		 Y
(vertical)		 Ejemplo Cuadrante
Positivo Positivo (3,2) I
Negativo Positivo (-4,3) II
Negativo Negativo (-2,-1) III
Positivo Negativo (2,-3) IV

 
La palabra cuadrante viene de cuad que significa cuatro. Por ejemplo, cuatro bebés que nacen a la vez se llaman cuatrillizos, y un animal de cuatro patas se llama cuadrúpedo)

Aquí tienes los cuatro cuadrantes en un gráfico:

Ejemplo: el punto "A" (3,2) está 3 unidades a la derecha y 2 arriba. Como x e y son positivos, el punto está en el "cuadrante I"

Ejemplo: el punto "C" (-2,-1) está 2 unidades horizontalmente en dirección negativa,
y 1 abajo (también dirección negativa). Como x e y son los dos negativos, el punto está en el "cuadrante III"

El origen

El punto (0,0) tiene el nombre especial de "el origen", y a veces se le llama con la letra "O".

Dimensiones: 1, 2, 3 y más...

Piensa en esto:

1 En la línea de números sólo se puede ir a izquierda o derecha, así que cualquier posición se indica con un número
2 Las coordenadas cartesianas indican direcciones izquierda-derecha y arriba-abajo, así cualquier posición se indica con dos números
3 ¿Cómo señalamos un punto en el mundo real (como la punta de tu nariz)? Necesitamos indicar izquierda-derecha, arriba-abajo y delante-detrás, eso son tres números, ¡o 3 dimensiones!

 

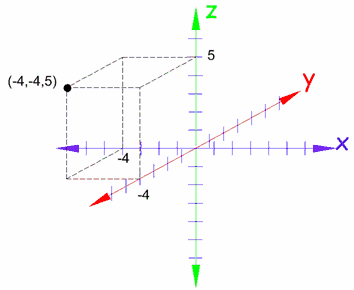
Y se pueden usar coordenadas cartesianas para localizar puntos en 3 dimensiones como en este ejemplo:

Aquí el punto (-4,-4,5) se indica en coordenadas cartesianas tridimensionales.

De hecho, esta idea se puede seguir en cuatro dimensiones y más... ¡Pero esto no te lo puedo enseñar con un dibujo!

 

 

Sigue

>>>Ecuaciones cuadráticas>>>

 

 

Para poder tomar los exámenes

de este tema debes estar

registrado, si no lo estás,

[Registrate aquí]

  

Fundación Educativa Héctor A. García