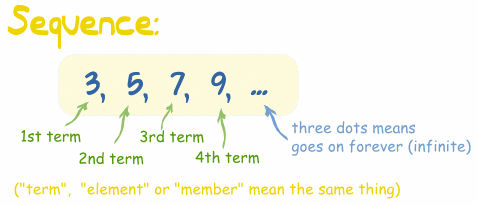|
|
Funciones, sucesiones y series, numeros irracionales y
más...

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
Entrar a exámenes
de:
Contenido Revisado 
|
|
¿Qué es una función?
 |
Una función es como una máquina: tiene una
entrada y una salida.
Y lo que sale
está relacionado de alguna manera con lo que
entra. |
Ejemplos
- "Multiplicar por
2" es una función muy simple
- La raíz cuadrada
(√) es una función
- Seno, coseno y
tangente son funciones que se usan en trigonometría
Pero no vamos a
ver funciones concretas...
... ahora
vamos a ver la idea general de una función.
Nombres
Primero, es útil darle
un nombre a una función. El nombre más común es "f",
pero puedes ponerle otros como "g" ... o
hasta "mermelada" si quieres.
Y también está bien
darle nombre a lo que se va adentro de la función, se
pone entre paréntesis () después del nombre de la
función:
Así que f(x)
te dice que la función se llama "f", y "x"
se pone dentro
Y normalmente verás lo
que la función hace a la entrada:
f(x) = x2
nos dice que la función "f"
toma "x" y lo eleva al cuadrado.

Así que con la función
"f(x) = x2", una entrada de 4 da una
salida de 16. De hecho podemos escribir f(4) = 16.
Nota: a veces las
funciones no tienen nombre, y puede que veas algo como
y = x2
Relacionar
Arriba dije que una
función es como una máquina. Pero una función no
tiene engranajes ni correas ni partes que se muevan. ¡Y
no destruye lo que pones dentro!
En realidad, una función
relaciona la entrada con la salida.
Decir que "f(4) = 16"
es como decir que 4 está relacionado de alguna manera
con 16. O también 4 → 16
 |
Ejemplo: este árbol crece 20 cm cada año, así
que la altura del árbol está relacionada
con la edad por la función a:
a(edad)
= edad × 20
Así que si la
edad es 10 años, la altura es a(10) = 200
cm |
Volveremos a esta idea
después de responder la pregunta...
¿Con qué tipo de cosas
trabaja una función?
Los
"números" parecen una respuesta clara, pero...
| |
 |
... ¿qué números? Por ejemplo, la función de la
altura del árbol a(edad) = edad×20
no tiene sentido si la edad es menor que cero. |
 |
... también podrían ser letras ("A"→"B"), o
códigos de identificación ("A6309"→"Acceso") o
cosas más raras. |
Así que tenemos que
usar algo más general, y ahí es donde entran en
juego los conjuntos:
|
|
Un
conjunto es una colección de cosas, por
ejemplo números.
Aquí tienes
algunos ejemplos:
El
conjunto de los números pares: {..., -4,
-2, 0, 2, 4, ...}
Un conjunto de ropa: {"sombrero","camisa",...}
El conjunto de los números primos: {2,
3, 5, 7, 11, 13, 17, ...}
Los múltiplos de 3 que son más pequeños
que 10: {3, 6, 9}
Cada cosa
individual en un conjunto (como "4" o
"sombrero") es un miembro, o
elemento. |
Así que una función
toma elementos de un conjunto, y devuelve (normalmente
con algún cambiados) elementos de un conjunto. Con esto
llegamos a la definición formal:
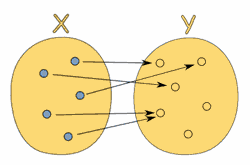 |
Definición
formal de función
Una función
relaciona cada elemento de un conjunto
con un elemento exactamente de otro conjunto
(puede ser el mismo conjunto).
|
| |
|
 |
"exactamente
uno" significa que la función es
univaluada. No devolverá 2 o más
resultados para la misma entrada. ¡Así que "f(2)
= 7 o 9" no vale! |
 |
Cada
elemento de "X" se relaciona con un elemento de
"Y". Decimos que la función cubre
"X" (relaciona cada elemento de)
|
También fíjate que en
el dibujo de arriba hay dos elementos en "X" que se
relacionan con el mismo elemento de "Y". No pasa nada.
No hay ninguna regla contra esto.
Y finalmente, fíjate en
que algunos elementos de "Y" no se relacionan con nada.
Eso también vale.
Esto
son cosas normales entre funciones, pero algunos tipos
de funciones cumplen reglas más estrictas, para saber
más lee sobre inyectivo, sobreyectivo y biyectivo
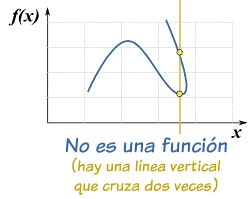 |
La prueba de
la línea vertical
En un gráfico,
la idea de univaluada significa que
ninguna línea vertical cruza más de una vez.
Si alguna
cruzara más de una vez no sería una
función. |
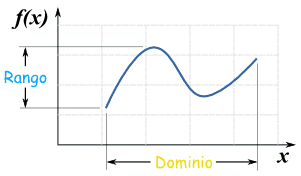
Dominio, codominio y
rango
En el dibujo de arriba
- el conjunto "X" es
el dominio,
- el conjunto "Y" es
el codominio, y
- el conjunto de
elementos de Y a los que llega alguna flecha (los
valores verdaderos de la función) se llama rango
o imagen.
Leete el siguiente
trabajo, para que sepas más de este tema:
Dominio,
codominio y rango
 |
En
su forma más simple el dominio son todos los
valores a los que aplicar una función, y el
rango son los valores que resultan.
Pero de hecho son
conceptos importantes cuando se define
una función. ¡Sigue leyendo! |
Por
favor, primero lee "¿Qué es una función?"...
Funciones
Una
función relaciona una entrada con una
salida.
 |
Ejemplo: este árbol crece 20 cm cada año, así
que la altura del árbol está relacionada
con la edad por la función a:
a(edad)
= edad × 20
Así que si la
edad es 10 años, la altura es a(10) = 200
cm |
Decir que "a(10)
= 200" es como relacionar 10 con 200. O bien 10 →
200
Entrada y salida
Pero muchas veces es
importante decir qué valores pueden entrar y
pueden salir de una función.
Aquí tienes algunas
razones:
- La función no
funciona si das valores equivocados (como una edad
negativa)
- Limitar los
valores de entrada te puede permitir hacer después
cosas especiales con la función
- Saber el tipo de
valores de salida (por ejemplo siempre positivos)
también ayuda
Entonces, ¿cómo
se dice lo que entra o sale en una función?
respuesta: se usan conjuntos...
|
|
Un
conjunto es una colección de cosas, por
ejemplo números.
Aquí tienes
unos ejemplos:
Conjunto
de números pares: {..., -4, -2, 0, 2, 4,
...}
Conjunto de números impares: {..., -3,
-1, 1, 3, ...}
Conjunto de números primos: {2, 3, 5, 7,
11, 13, 17, ...}
Múltiplos positivos de 3 que son menores
que 10: {3, 6, 9}
|
De hecho, las
funciones se definen sobre conjuntos:
 |
Definición
formal de una función
Una función
relaciona cada elemento de un conjunto
con exactamente un elemento de otro conjunto
(puede ser el mismo conjunto).
|
Dominio y rango
Hay nombres especiales
para lo que puede entrar, y también lo que
puede salir de una función:
  |
Lo que
puede entrar en una función se llama el
dominio |
  |
Lo que
es posible que salga de una función se
llama el codominio |
  |
Lo que
en realidad sale de una función se llama
rango o imagen |
Entonces, en el
diagrama de arriba el conjunto "X" es el dominio, el
conjunto "Y" es el codominio, y los elementos de Y a los
que llegan flechas (los valores producidos realmente por
la función) son el rango.
Parte de la función
Lo que sale (el
rango) depende de lo que pones (el dominio),
pero TÚ defines el dominio.
De hecho el dominio es
una parte esencial de la función. Un dominio diferente
da una función diferente.
Ejemplo: una simple
función como f(x) = x2 puede tener dominio
(lo que entra) los números de contar {1,2,3,...}, y el
rango será entonces el conjunto {1,4,9,...}
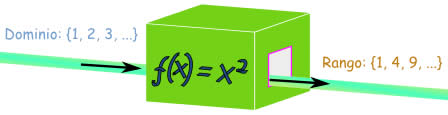
Y otra función g(x) = x2
puede tener como dominio los enteros
{...,-3,-2,-1,0,1,2,3,...}, entonces el rango será el
conjunto {0,1,4,9,...}

 |
Aunque las dos funciones toman la entrada y la
elevan al cuadrado, operan en conjuntos
diferentes de entradas, y por eso dan
salidas diferentes. |
| |
|
 |
También tienen diferentes propiedades.
Por ejemplo f(x)
siempre da resultados distintos, pero g(x) puede
dar la misma respuesta para dos entradas (como
g(-2)=4 y g(2)=4) |
Así que el dominio es
una parte muy importante de la función.
Entonces, ¿todas las
funciones tienen su dominio?
Sí, pero en matemáticas
sencillas no lo notas, porque el dominio se supone:
- Normalmente se
supone que es algo así como "todos los números que
hacen que funcione".
- O si estás
estudiando números enteros, el dominio será los
enteros.
- etc.
¡Pero en matemáticas
más avanzadas tienes que tener cuidado!
Codominio y rango
El codominio y el rango
tienen que ver con la salida, pero no son exactamente lo
mismo.
El codominio es el
conjunto de valores que podrían salir.
El rango es el conjunto
de valores que realmente salen.
Ejemplo: puedes
definir una función f(x)=2x con
dominio y codominio los enteros (porque tú lo eliges
así).
Pero si lo piensas,
verás que el rango (los valores que salen de verdad)
son sólo los enteros pares.
Así que el
codominio son los enteros (lo has elegido tú) pero
el rango son los enteros pares.
Así que rango es un
subconjunto del codominio.
¿Por qué los
dos? Bueno, a veces no conoces
exactamente el rango (porque la función es
complicada o no es conocida del todo), pero sabes el
conjunto en el que está (como los enteros
o los reales). Así que defines el codominio y sigues
trabajando.
La importancia del
codominio
Déjame que te haga una
pregunta: ¿la raíz cuadrada es una función?
Si tú dices que el
codominio (las salidas posibles) es el conjunto de
los números reales, ¡entonces la raíz cuadrada no
es una función! ... ¿te sorprende?
La razón es que
podría haber dos respuestas para una entrada, por
ejemplo f(9) = 3 o
-3
Una función debe ser
univaluada. No puede dar 2 resultados
para el mismo valor de entrada. ¡Por ejemplo "f(2) =
7 o 9" no está bien!
Pero se puede arreglar
simplemente limitando el codominio a los números
reales no negativos.
√De
hecho, el símbolo radical (como en √x)
siempre significa la raíz cuadrada positiva (la
principal), así que √x es una función porque
su codominio es correcto.
Así que el codominio
que elijas puede afectar el que algo sea o no una
función.
Notación
A los matemáticos no
les gusta escribir muchas palabras cuando unos pocos
símbolos hacen el mismo trabajo. Así que hay maneras de
decir que "el dominio es", "el codominio es", etc.
Esta es la mejor manera
que conozco:
|
|
Esto dice que la función "f" tiene
dominio "N" (los números naturales), y
también codominio "N". |
|
|
y
esto dice que la función "f" toma "x" y devuelve
"x2" |
Pares ordenados
Puedes escribir las
entradas y salidas de una función como "pares ordenados",
como (4,16).
Se llaman pares
ordenados porque la entrada siempre va primero y la
salida después.
Así que (4,16) significa
que la función toma "4" y devuelve "16"
Y una función se puede
definir como un conjunto de pares ordenados:
Ejemplo: {(2,4),
(4,5), (7,3)} es una función que dice que "2 se
relaciona con 4", "4 se relaciona con 5" y "7 se
relaciona con 3".
Fíjate también en que el dominio es {2,4,7} y el
rango es {4,5,3}
Pero la función debe
ser univaluada, esto se puede decir
"si contiene (a, b) y (a,
c), entonces b tiene que ser igual a c"
Es otra manera de decir
que una entrada "a" no puede dar dos resultados
diferentes.
Ejemplo: {(2,4),
(2,5), (7,3)} no es una función
porque {2,4} y {2,5} quieren decir que 2 estaría
relacionado con 4 y 5, o sea
no es univaluada
Conclusión
- una función
relaciona entradas con salidas
- una función
toma elementos de un conjunto (el dominio)
y los relaciona con elementos de un conjunto (el
codominio).
- las salidas
(los verdaderos valores de la función) se llaman
la imagen o rango
- una entrada
sólo produce una salida (no una u otra)
- una entrada y
la salida que corresponde se llaman juntos un
par ordenado
- así que una
función también se puede ver como un conjunto
de pares ordenados
Sucesiones y series
Puedes leer una introducción sencilla a las sucesiones
en pautas comunes de números.
¿Qué es una sucesión?
Una sucesión
es un conjunto de cosas (normalmente números) una detrás
de otra, en un cierto orden.
Patrones conocidos de
números
A veces
los números forman patrones interesantes. Aquí mostramos
los más comunes y cómo se forman.
Sucesiones aritméticas
Una sucesión
aritmética se construye sumando un valor fijo cada
vez.
Ejemplos:
|
1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
Esta sucesión tiene
una diferencia de 3 entre cada dos números
consecutivos.
El patrón se sigue sumando 3 al último número cada
vez.
| 3,
8, 13, 18, 23, 28, 33, 38,
... |
Esta sucesión tiene
una diferencia de 5 entre cada dos números
consecutivos.
El patrón se sigue sumando 3 al último número cada
vez.
Sucesiones geométricas
Una sucesión geométrica
se construye multiplicando un valor fijo cada vez.
Ejemplos:
| 2,
4, 8, 16, 32, 64, 128, 256,
... |
Esta sucesión tiene un
factor 2 entre cada dos números consecutivos.
El patrón se sigue multiplicando el último número
por 2 cada vez.
| 3,
9, 27, 81, 243, 729, 2187,
... |
Esta sucesión tiene un
factor 3 entre cada dos números consecutivos.
El patrón se sigue multiplicando el último número
por 3 cada vez.
Sucesiones especiales
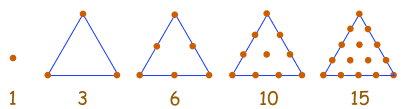
Números triangulares
| 1,
3, 6, 10, 15, 21, 28, 36, 45,
... |
Esta sucesión se genera
con un patrón de puntos que forma un triángulo.
Añadiendo otra fila de puntos y contando el total se
encuentra el siguiente número de la sucesión.
Números
cuadrados
| 1,
4, 9, 16, 25, 36, 49, 64, 81,
... |
El siguiente número se
hace elevando su posición al cuadrado.
El segundo número es 2 al cuadrado (22 o 2×2)
El séptimo número es 7 al cuadrado (72 o 7×7)
etc.
Números
cúbicos
| 1,
8, 27, 64, 125, 216, 343, 512, 729,
... |
El siguiente número se
calcula elevando su posición al cubo.
El segundo número es 2 al cubo (23 o 2×2×2)
El séptimo número es 7 al cubo (73 o 7×7×7)
etc.
Números de
Fibonacci
| 0,
1, 1, 2, 3, 5, 8, 13, 21, 34,
... |
El siguiente número se
halla sumando los dos números delante de él.
El 2 se calcula sumando los dos números delante de él
(1+1)
El 21 se calcula sumando los dos números delante de él
(8+13)
El siguiente número de la sucesión sería 55 (21+34)
¿Puedes averiguar algunos números más?
Otras sucesiones
¡Hay muchas más!
Incluso se te pueden ocurrir a ti ...
Finita o infinita
Si
la sucesión sigue para siempre, es una sucesión
infinita,
si no es una sucesión finita
Ejemplos
{1, 2, 3, 4 ,...} es
una sucesión muy simple (y es una sucesión
infinita)
{20, 25, 30, 35, ...}
también es una sucesión infinita
{1, 3, 5, 7} es la
sucesión de los 4 primeros números impares (y es una
sucesión infinita)
{4, 3, 2, 1} va de
4 a 1 hacia atrás
{1, 2, 4, 8, 16,
32, ...} es una sucesión infinita donde vamos
doblando cada término
{a, b, c, d,
e} es la sucesión de las 5 primeras letras
en order alfabético
{a, l, f, r, e, d,
o} es la sucesión de las letras en el nombre "alfredo"
{0, 1, 0, 1, 0, 1,
...} es la sucesión que alterna 0s y 1s (sí,
siguen un orden, en este caso un orden alternativo)
En orden
Cuando decimos que los
términos están "en orden", ¡nosotros somos los que
decimos qué orden! Podría ser adelante, atrás...
o alternando... ¡o el que quieras!
Una sucesión es muy
parecida a un conjunto, pero con los términos en
orden (y el mismo valor sí puede aparecer muchas
veces).
Ejemplo: {0, 1, 0, 1,
0, 1, ...} es la sucesión que alterna 0s y
1s. El conjunto sería sólo {0,1}
La regla
Una sucesión sigue una
regla que te dice cómo calcular el valor de cada
término.
Ejemplo: la sucesión
{3, 5, 7, 9, ...} empieza por 3 y salta 2 cada vez:
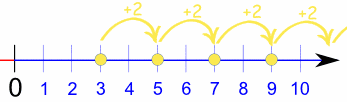
¡Pero la regla debería
ser una fórmula!
Decir que "empieza
por 3 y salta 2 cada vez" no nos dice cómo se
calcula el:
- 10º término,
- 100º término, o
-
n-ésimo término (donde n
puede ser cualquier número positivo que queramos).
Así que queremos una
fórmula con "n" dentro (donde n será la posición que
tiene el término).
Entonces, ¿cuál sería
la regla para {3, 5, 7, 9, ...}?
Primero, vemos que la
sucesión sube 2 cada vez, así que podemos adivinar que
la regla va a ser "2 × n". Vamos a verlo:
Probamos la regla: 2n
| n |
Término |
Prueba |
| 1 |
3 |
2n
= 2×1 = 2 |
| 2 |
5 |
2n
= 2×2 = 4 |
| 3 |
7 |
2n
= 2×3 = 6 |
Esto casi
funciona... pero la regla da todo el tiempo valores 1
unidad menos de lo que debería, así que vamos a
cambiarla un poco:
Probamos la regla: 2n+1
| n |
Término |
Regla |
| 1 |
3 |
2n+1
= 2×1 + 1 = 3 |
| 2 |
5 |
2n+1
= 2×2 + 1 = 5 |
| 3 |
7 |
2n+1
= 2×3 + 1 = 7 |
¡Funciona!
Así que en vez de decir
"empieza por 3 y salta 2 cada vez" escribimos la regla
como
La regla para {3, 5, 7, 9, ...} es:
2n+1
Ahora, por
ejemplo, podemos calcular el término 100º: 2 ×
100 + 1 = 201
Sigue
>>>Funciones,
sucesiones y series, numeros irracionales y más...>>>

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
|
|