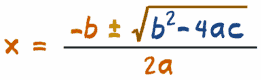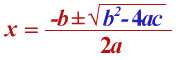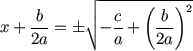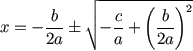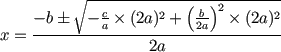|
|
Ecuación cuadrática

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
Entrar a exámenes
de:
Contenido Revisado 
|
|
Ecuación cuadrática
| Esto es una
ecuación cuadrática: |
 |
|
(a, b,
y c pueden tener cualquier valor, excepto
que a no puede ser 0.) |
 |
La letra "x"
es la variable o incógnita, y las
letras a, b y c son los coeficientes
(lee las Definiciones básicas de Álgebra) |
 |
Y el nombre
cuadrática viene de "cuad" que quiere
decir cuadrado, porque el exponente más
grande es un cuadrado (en otras palabras
x2). |
Ejemplos de ecuaciones
cuadráticas:
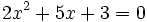 |
|
En esta a=2, b=5 y
c=3 |
|
|
|
|
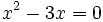 |
|
Aquí hay una un
poco más complicada:
- ¿Dónde
está a? En realidad a=1,
porque normalmente no escribimos "1x2"
-
b=-3
- ¿Y dónde
está c? Bueno, c=0, así que no
se ve.
|
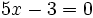 |
|
¡Ups!
Esta no es una ecuación cuadrática,
porque le falta el x2 (es decir
a=0, y por eso no puede ser cuadrática) |
¿Qué tienen de
especial?
Las ecuaciones
cuadráticas se pueden resolver usando una fórmula
especial llamada fórmula cuadrática:
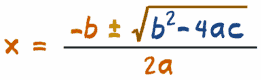
 |
El "±" quiere
decir que tienes que hacer más Y menos, ¡así
que normalmente hay dos soluciones! |
|
|
|
 |
La parte azul
(b2 - 4ac) se llama
discriminante, porque sirve para
"discriminar" (decidir) entre los tipos
posibles de respuesta:
- si es
positivo, hay DOS soluciones
- si es
cero sólo hay UNA solución,
- y si
es negativo hay dos soluciones que
incluyen números imaginarios .
|
Solución
Para resolverla, sólo
pon los valores de a,b y c en la fórmula cuadrática y
haz los cálculos.
Ejemplo: resuelve
5x² + 6x + 1 = 0
Fórmula
cuadrática: x = [ -b ± √(b2-4ac)
] / 2a
Los
coeficientes son: a = 5, b
= 6, c = 1
Sustituye
a,b,c: x = [ -6 ± √(62-4×5×1)
] / 2×5
Resuelve:
x = [ -6 ± √(36-20) ]/10 = [ -6 ± √(16) ]/10 = ( -6
± 4 )/10
Respuesta:
x = -0.2 and -1
(Comprobación:
5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 =
0.2 -1.2 + 1 = 0
5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 +
1 = 0)
Ecuaciones cuadráticas
disfrazadas
Algunas ecuaciones no
parece que sean cuadráticas, pero con manipulaciones
astutas se pueden transformar en una:
|
Disfrazadas |
Qué hacer |
En forma
estándar |
a, b y c |
|
x2
= 3x -1 |
Mueve todos
los términos a la izquierda |
x2
- 3x + 1 = 0 |
a=1, b=-3, c=1 |
|
2(x2
- 2x) = 5 |
Desarrolla
paréntesis |
2x2
- 4x - 5 = 0 |
a=2, b=-4,
c=-5 |
|
x(x-1) = 3 |
Desarrolla
paréntesis |
x2
- x - 3 = 0 |
a=1, b=-1,
c=-3 |
|
5 + 1/x - 1/x2
= 0 |
Multiplica por x2 |
5x2
+ x - 1 = 0 |
a=5, b=1, c=-1 |
Derivación de la fórmula cuadrática
Esta es la forma de una
ecuación cuadrática:
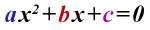
Y se puede resolver con
la fórmula cuadrática:
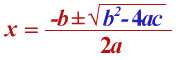
Esta fórmula parece
mágica, pero ahora puedes seguir los pasos para ver de
dónde viene.
1. Completar el
cuadrado
Es difícil manejar una
ecuación donde "x" aparece dos veces, pero hay una
manera de arreglarla para que "x" aparezca una sola vez.
Se llama "completar el cuadrado" (¡por favor léelo
primero!).
Vamos a
aprovechar lo que pasa cuando desarrollas (x+d)2
(x+d)2
= (x+d)(x+d) = x(x+d) + d(x+d) =
x2 + 2dx + d2
|
Así que si
podemos poner la ecuación en la forma: |
|
|
x2
+ 2dx + d2
|
|
|
Entonces la
podemos reescribir así: |
|
|
(x+d)2
|
|
|
Y esto hará el
resto del trabajo más fácil |
Vamos:
2. Ahora resolvemos "x"
Ahora vamos a reordenar
la ecuación para dejar "x" a la izquierda
| Empieza por |
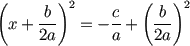 |
| Raíz cuadrada |
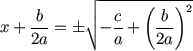 |
| Mueve b/2a a
la derecha |
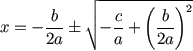 |
¡Ya está resuelto! Pero vamos a simplificar un
poco:
|
| Multiplicamos
a la derecha por 2a/2a |
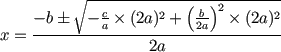 |
| Simplificamos: |
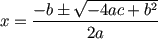 |
Y esta es la fórmula cuadrática que conocemos y
que tanto nos gusta:
|
| |
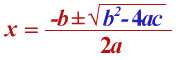 |
Solucionador de ecuaciones cuadráticas
| Si tienes
una ecuación de la forma "ax2 + bx
+ c = 0", nosotros te la resolvemos. Sólo
entra los valores a, b y c debajo y pulsa "Ver
resultado" |
¿Es cuadrática?
Sólo si se puede poner
en la forma ax2 + bx + c = 0, y
a no es cero.
El nombre viene de "cuad"
que significa cuadrado, así que la mejor pista es que la
potencia sea un cuadrado (en otras palabras x2).
Todas estas son
ecuaciones cuadráticas disfrazadas:
|
Disfrazada |
En forma
estándar |
a, b y c |
|
x2
= 3x -1 |
x2
- 3x + 1 = 0 |
a=1, b=-3, c=1 |
|
2(x2
- 2x) = 5 |
2x2
- 4x - 5 = 0 |
a=2, b=-4,
c=-5 |
|
x(x-1) = 3 |
x2
- x - 3 = 0 |
a=1, b=-1,
c=-3 |
|
5 + 1/x - 1/x2
= 0 |
5x2
+ x - 1 = 0 |
a=5, b=1, c=-1 |
¿Cómo funciona?
La(s) solucion(es) de
una ecuación cuadrática se pueden calcular con la
fórmula cuadrática:
El "±" significa que
tienes que hacer más Y menos, ¡así que normalmente hay
dos soluciones!
La parte azul (b2
- 4ac) se llama "discriminante", porque sirve para
"discriminar" (decidir) entre los tipos posibles de
respuesta. Si es positivo, hay DOS soluciones, si es
cero sólo hay UNA solución, y si es negativo hay
soluciones imaginarias.
Completar el cuadrado
"Completar el cuadrado"
es cuando...
|
... tenemos
una ecuación cuadrática como: |
 |
y la ponemos
en esta forma: |
|
ax2
+ bx + c = 0 |
a(x+d)2
+ e = 0 |
|
Para los que tengáis prisa, os puedo decir ya
que: |
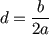
|
, y: |
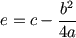 |
Pero si tienes tiempo, deja que te explique cómo llegar
allá.
La pista
Primero tengo que
enseñarte lo que pasa cuando desarrollas (x+d)2
(x+d)2
= (x+d)(x+d) = x(x+d) + d(x+d) =
x2 + 2dx + d2
|
Así que si
podemos poner la ecuación en la forma: |
|
|
x2
+ 2dx + d2
|
|
|
Entonces
podemos escribirla inmediatamente como: |
|
|
(x+d)2
|
|
|
Que está
bastante cerca de lo que queremos, el
trabajo estaría casi hecho |
El caso más simple
|
Vamos a
trabajar primero con: |
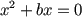 |
|
Suma (b/2)2
a los dos lados: |
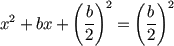 |
Ahora mira la "pista" de arriba y piensa en
que 2d=b así que d=b/2
Sí, está en la forma x2 +
2dx + d2 donde d=b/2,
así que lo volvemos a escribir
|
|
Completamos el
cuadrado: |
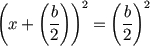 |
|
|
|
|
¿Ves? No es
difícil. Con truco pero no difícil. |
El completo
Ahora vamos al caso
completo:
|
Fíjate en que
tenemos: |
|
a(x+d)2
+ e = 0
|
|
Donde: |
|
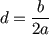
|
, y: |
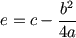 |
|
Ejemplo
Vamos a probar con un
ejemplo de verdad:
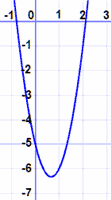 |
Pero pasa algo interesante... el vértice (el
punto más alto o más bajo de la curva) está en
(2/3, -19/3) ... ¡y esos números aparecen
en la ecuación!
Otra cosa es que ahora podemos resolver la
ecuación a mano:
|
¿Para qué "completar
el cuadrado"?
¿Para qué querrías
completar el cuadrado cuando basta usar la fórmula
cuadrática para resolver una eciación cuadrática?
Bueno, la respuesta
está arriba en parte, donde la forma nueva te da el
vértice, y también hace la ecuación fácil de
resolver.Es
el primer paso en la derivación de la fórmula
cuadrática
A veces la forma
"ax2 + bx + c" puede ser parte de un
problema más grande y escribirla como "a(x+d)2
+ e" hace más fácil llegar a la solución,
porque la "x" sólo aparece una vez.
Por ejemplo es
difícil integrar 1/(3x2 - 4x - 6) pero
1/(3(x - 4/6)2 - 22/3) es más fácil.
O "x" puede ser una
función (como cos(z)) y de nuevo reescribir
puede abrirte un camino mejor a la solución.
Es sólo otra
herramienta en tu caja de herramientas matemáticas.
Sigue
>>>Funciones,
sucesiones y series, numeros irracionales y más...>>>

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
|
|