|
Polinomios
Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
Entrar a exámenes
de:
Contenido Revisado 
|
|
Polinomios
Un
polinomio es así:
 |
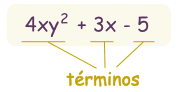un ejemplo
de polinomio
este tiene 3 términos |
Están
hechos de:
 |
constantes (como 3,
-20, o ½) |
|
|
variables (como x
e y) |
|
|
exponentes (como el 2 en y2)
pero sólo pueden ser 0, 1, 2, 3, ... etc |
Que se
pueden combinar usando:
|
+ - × |
sumas, restas y
multiplicaciones... |
|
|
... ¡pero no divisiones!
|
Estas
reglas hacen que los polinomios sean simples, ¡así es
fácil trabajar con ellos!
¿Son polinomios o no?
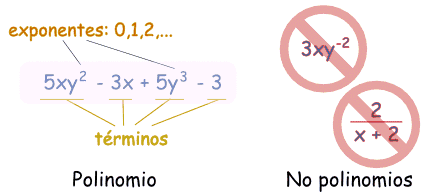
Estos son
polinomios:
- 3x
- x - 2
- 3xyz + 3xy2z
- 0.1xz - 200y + 0.5
Y estos no son
polinomios
- 2/(x+2) no
lo es, porque dividir no está permitido
- 3xy-2
no lo es, porque un exponente es "-2" (los
exponentes sólo pueden ser 0,1,2,...)
Pero esto sí
está permitido:
- x/2 está
permitido, porque también es (½)x (la
constante es ½, o 0.5)
- también 3x/8
por la misma razón (la constante es 3/8, o 0.375)
Monomios, binomios,
trinomios
Hay nombres especiales
para los polinomios con 1, 2 o 3 términos:
¿Cómo te
aprendes los nombres?
¡Piensa en bicicletas! |
 |
(También existen
cuatrinomio (4 términos) y quintinomio (5 términos),
pero se usan poco)
Muchos términos
Los polinomios pueden
tener montones de términos, pero no infinitos
términos.
¿Qué tienen de
especial los polinomios?
Por su definición tan
estricta, es fácil trabajar con polinomios.
Por ejemplo sabemos
que:
- Si sumas o restas
polinomios te sale un polinomio
- Si multiplicas
polinomios te sale un polinomio
Así que puedes hacer
muchas sumas y multiplicaciones con ellos, y siempre
sale un polinomio al final.
Grado
El grado de un
polinomio con una sola variable es el mayor exponente
de esa variable.
Ejemplo:
 |
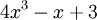El
grado es 3 (el mayor exponente de
x) |
Sumar y
restar polinomios
Un
polinomio es algo así como esto:
|
|
ejemplo de
polinomio
este tiene 3 términos |
Para sumar polinomios
simplemente suma juntos los términos similares...
¿qué son términos similares?
Términos similares
"Términos similares"
son términos cuyas variables (y sus exponentes
como el 2 en x2) son los mismos.
En otras palabras,
términos que "se parecen".
Ejemplos:
|
Términos |
Por qué
son "similares" |
 |
7x |
x |
-2x |
porque las
variables son todas x |
|
|
(1/3)xy2 |
-2xy2
|
6xy2
|
porque las
variables son todas xy2 |
Sumar polinomios
Dos pasos:
- Pon juntos los
términos similares
- Suma los términos
similares
Ejemplo: suma
2x2 + 6x + 5 y 3x2
- 2x - 1
Junta los términos similares: 2x2 + 3x2
+ 6x - 2x + 5 - 1
Suma los términos similares: (2+3)x2
+ (6-2)x + (3-1)
= 5x2 +
4x + 4
Aquí tienes una
animación que te lo enseña
Multiplicar polinomios
Un
polinomio es algo así como esto:
|
|
ejemplo de
polinomio
este tiene 3 términos |
Para multiplicar dos
polinomios:
- multiplica cada
término de un polinomio por cada término
del otro polinomio
- suma las
respuestas, y simplifica si hace falta
Veamos primero los
casos más simples
1 término × 1 término
(monomio por monomio)
Para multiplicar un
término por otro, primero multiplica las constantes,
después multiplica cada variable y combina el
resultado
Expresiones racionales
Una expresión que es
cociente de dos polinomios:
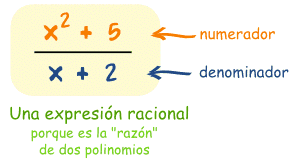
Otros ejemplos:
En general
Una función racional es
el cociente de dos polinomios P(x) y Q(x) así
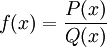
Excepto que Q(x) no
puede ser cero (y cualquier valor de x que hace Q(x)=0
no está definido)
Conjugar
El conjugado es cuando
cambias el signo que está entre dos términos,
así:
Sólo se usa en
expresiones con dos términos (llamadas
"binomios")
Otros ejemplos:
|
Expresión |
Su conjugado |
|
x2 - 3 |
x2 + 3 |
|
a + b |
a - b |
|
a - b3 |
a + b3 |
Ejemplos de uso
El conjugado puede ser
muy útil porque...
...
cuando multiplicas algo por su conjugado salen
cuadrados así:
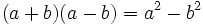
¿Para qué vale eso?
Puede ayudarte a mover
una raíz cuadrada de la parte de abajo (denominador) de
una fracción a la parte de arriba (numerador) o al
revés. Ahora te enseño cómo.
 |
Nota:
muchas raíces cuadradas son números
irracionales, así que este proceso se llama "Racionalizar
el Denominador" |
Ejemplo: aquí
tienes una fracción con "denominador irracional":
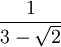
¿Cómo pasamos la
raíz de 2 arriba?
Respuesta:
Multiplica arriba y abajo por el conjugado
(esto no cambia el valor de la fracción), así:
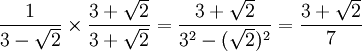
(¿Viste cómo el denominador se convirtió en "a2-b2"?)
Hay otro ejemplo en la
página evaluar límites donde muevo una raíz cuadrada del
numerador al denominador.
Así que intenta
recordar este truco, ¡te puede ayudar algún día a
resolver una ecuación!
Racionalizar el denominador
¿Qué es?
"Racionalizar el
denominador" es cuando mueves una raíz (por ejemplo una
raíz cuadrada o cúbica) de la parte de abajo de una
fracción a la de arriba.
¿Por qué se llama
"racionalizar el denominador" ?
|
|
La parte de
abajo de una fracción se llama denominador, y
muchas raíces son irracionales, así que (por
ejemplo) esto:
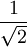
tiene
"denominador irracional" (√2 es
irracional). |
¡Para ponerla de la
"forma más simple" no debería haber ningún número
irracional en el denominador!
Así que arreglarla
(haciendo el denominador racional) se llama "racionalizar
el denominador"
Entonces... ¿Cómo se
hace?
1. Multiplica arriba y
abajo por una raíz
A veces basta con
multiplicar arriba y abajo por una raíz:
Ejemplo:
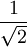tiene denominador irracional. Vamos a arreglarlo.
Multiplica arriba y
abajo por la raíz cuadrada de 2, porque: √2 × √2 =
2:
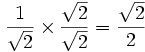
Ahora el
denominador es un número racional (=2). ¡Hecho!
Nota: no pasa nada si
tienes un número irracional arriba (en el numerador) de
una fracción.
2. Multiplica arriba y
abajo por el conjugado
Hay otra manera
especial de mover una raíz cuadrada de abajo a arriba en
una fracción... multiplicas arriba y abajo por el
conjugado del denominador.
El conjugado es cuando
cambias el signo de en medio de dos términos:
|
Expresión de
ejemplo |
Su conjugado |
|
x2
- 3 |
x2
+ 3 |
|
a + b3 |
a - b3 |
Aquí tienes cómo se
hace:
Ejemplo: aquí
tienes una fracción con "denominador irracional":
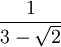
¿Cómo movemos la
raíz cuadrada de 2 arriba?
Repuesta:
Multiplica arriba y abajo por el conjugado
(esto no cambia el valor de la fracción), así:
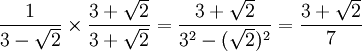
Intenta recordar estos
trucos, ¡te pueden ayudar un día a resolver una
ecuación!
Sigue
>>>Ecuaciones
lineales>>>
Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
|
