|
Simpiflicar

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
Entrar a exámenes
de:
Contenido Revisado 
|
|
Multiplicación
de Negativos
Cuando Multiplicas ...
| |
|
|
Example |
 ×
×
 |
dos positivos,
obtienes un positivo: |
 |
3 × 2 = 6 |
| |
|
|
|
 ×
×
 |
Un positivo y un
negativo,obtienes un negativo: |
 |
(-3) × 2 = -6 |
| |
|
|
|
 ×
×
 |
Un negativo y un
positivo obtienes un negativo: |
 |
3 × (-2) = -6 |
| |
|
|
|
 ×
×
 |
Dos negativos,
obtienes un positivo: |
 |
(-3) × (-2) = 6 |
Entonces,
un negativo multiplicado por un positivo da un negativo…
¡Pero, multiplicar dos negativos da un positivo!
¿Por qué la
multiplicación de dos negativos da un positivo?
Bien, para empezar hay
una explicación que tiene que ver con el “sentido común”:
Si yo digo “¡Come!”,
estoy estimulándote a que comas (positivo), pero si digo
“¡No comas!” estoy haciendo lo opuesto (negativo).
Ahora, si digo: “No no
comas” (es decir, no dejes de comer), estoy diciendo que
no quiero que mueras de hambre, por lo tanto es como si
estuviera diciendo nuevamente “¡Come!”.
Entonces, dos negativos
dan un positivo y si con esta explicación es suficiente,
entonces no necesitas seguir leyendo.
Dirección
Todo depende de la
dirección. ¿Te acuerdas de la Línea de Números?

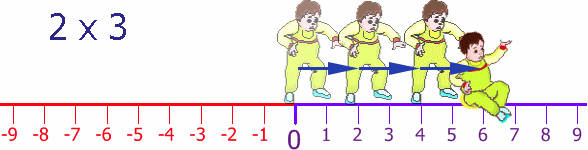
Bien, aquí tenemos al
bebé Esteban dando sus primeros pasitos. Da dos pasitos
por vez y hace esto tres veces, entonces se mueve 3 x 2
= 6 pasos hacia delante:
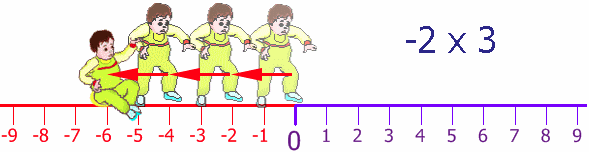
Ahora, el bebé Esteban
también puede caminar hacia atrás (¡es un bebito
inteligente!). Su papá lo coloca nuevamente en el
principio y entonces Esteban da dos pasos hacia atrás y
hace esto tres veces:
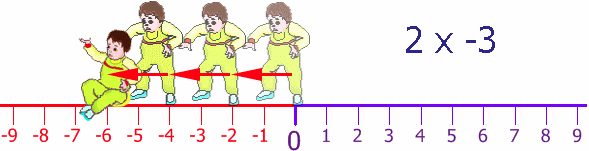
Una vez más el papá de
Esteban lo coloca en el principio pero mirando hacia el
lado opuesto. Esteban da dos pasos hacia adelante (¡para
él!) pero en realidad se está dirigiendo hacia la
dirección negativa. Hace esto tres veces:
Nuevamente en el
comienzo (¡gracias a papá!) y aún de frente a la
dirección negativa, intenta caminar hacia atrás y una
vez más da dos pasos a la vez. Hace esto tres veces:
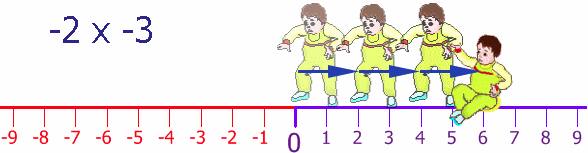
Así, si camina hacia
atrás de frente a la dirección negativa, se mueve hacia
la dirección positiva.
Más Ejemplos
Tener Dinero o Deber
Dinero
Ejemplo: debes $5 a
cada una de tres personas. Así que tienes "15
negativos" (3 × -5 = -15).
Si entonces te
dicen "nos gustas tanto que te perdonamos las deudas"...
se te acaban de quitar tres veces -5, así que es
como si ganaras $15 (-3 × -5 = +15).
Niveles de Agua que
Suben/Bajan
Ejemplo: el tanque
tiene 30,000 litros, y se sacan 1,000 todos los días.
¿Cuál era el nivel hace 3 días?
Sabemos que el
tanque gana -1,000 cada día, y tenemos que restar
esto tres veces, así que el cambio será:
-3 ×
-1,000 = +3,000
El cálculo completo
es:
30,000 + (-3 × -1,000) = 30,000 + 3,000 = 33,000
¡Y eso es todo!
Leyes
asociativa, conmutativa y distributiva
¡Uf!
¡Vaya palabrejas! Pero la idea es simple.
Leyes conmutativas
Las "leyes conmutativas"
sólo quieren decir que puedes intercambiar los números
cuando sumas o cuando multiplicas y la
respuesta va a ser la misma.
a + b = b + a
a × b = b × a
Ejemplos:
| Puedes
intercambiarlos cuando sumas: |
3 + 6 = 6 + 3
|
| Puedes
intercambiarlos cuando multiplicas: |
2 × 4 = 4 × 2
|
Leyes asociativas
Las "Leyes asociativas"
quieren decir que no importa cómo agrupes los números (o
sea, qué calculas primero) cuando sumas o cuando
multiplicas.
(a + b) + c = a + (b +
c)
(a × b) × c = a × (b × c)
Ejemplos:
| Esto: |
(2 + 4)
+ 5 = 6 + 5
= 11 |
| da el
mismo resultado que esto: |
2 + (4 + 5) = 2 +
9 = 11 |
| Esto: |
(3 × 4) ×
5 = 12 × 5
= 60 |
| da el
mismo resultado que esto: |
3 × (4 × 5) = 3
× 20 = 60 |
Usos:
A veces es más fácil sumar
o multiplicar si cambiamos el orden:
| ¿Cuánto es
19 + 36 + 4? |
| 19 + 36 +
4 = 19 + (36 + 4) = 19 + 40
= 59 |
O si los reordenamos
un poco (fíjate que aquí usamos también la ley
conmutativa para eso):
| ¿Cuánto
es 2 × 16 × 5? |
| 2 × 16
× 5 = (2 × 5) × 16 = 10
× 16 = 160 |
Ley distributiva
La "ley distributiva"
es la MEJOR de todas, pero hay que usarla con mucho
cuidado.
Quiere decir que la
respuesta es la misma cuando:
- sumas
varios números y el resultado lo multiplicas
por algo, o
- haces cada
multiplicación por separado y luego sumas
los resultados
Así:
(a + b) × c = a × c
+ b × c
Ejemplos:
| Esto: |
(2 + 4) ×
5 = 6 × 5
= 30 |
| da el
mismo resultado que esto: |
2×5 + 4×5
= 10 + 20
= 30 |
| Esto: |
(6 - 4) ×
3 = 2 × 3
= 6 |
| da el
mismo resultado que esto: |
6×3 - 4×3
= 18 - 12
= 6 |
Usos:
A veces es más fácil
si rompemos una multiplicación difícil:
| ¿Cuánto
es 204 × 6? |
| 204 ×
6 = 200×6 + 4×6 = 1,200 + 24 =
1,224 |
O para combinar:
| ¿Cuánto
es 6 × 16 + 4 × 16? |
| 6 × 16
+ 4 × 16 = (6+4) × 16 = 10
× 16 = 160 |
Resumen
|
Leyes conmutativas: |
a + b = b + a
a × b = b × a |
|
Leyes asociativas: |
(a + b) + c = a
+ (b + c)
(a × b) × c = a × (b × c) |
|
Ley distributiva: |
(a + b) × c = a
× c + b × c |
Multiplicar en cruz
|
Multiplicar en
cruz es ir de esto: |
|
|
|
|
|
A esto: |
8 × 3 = 12 × 2
|
¿Cómo funciona?
Bueno, si multiplicas
una fracción arriba y abajo por la misma cantidad,
no cambia su valor.
En este ejempo he
multiplicado la primera fracción arriba y abajo por el
número de abajo de la segunda fracción.
También podríamos haber
multiplicado la segunda fracción arriba y abajo
por el número de abajo de la primera fracción.
|
Ejemplo (la
segunda fracción de arriba): |
|
Y tendríamos:
|
8
× 3 |
= |
2
× 12 |
| |
|
|
12
× 3 |
3
× 12 |
¡Y magia! ¡Ahora los
números de abajo de las dos fracciones son
12 × 3 ... !
Podemos quitar los
12 × 3 (porque estamos
dividiendo los dos lados entre la misma cantidad) y la
ecuación todavía se cumple:
8 × 3 = 12 × 2
¡Hecho!
(En la práctica es más fácil saltarse los pasos
intermedios y pasar directamente a la forma de "producto
en cruz").
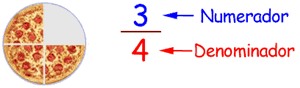 |
Terminología
He estado
diciendo "arriba" y "abajo" en las fracciones...
pero las palabras correctas son numerador
y denominador, ¿vale?
Sólo quería
hacerlo simple. |
Usando variables
Hasta ahora hemos usado
un ejemplo real, pero se puede escribir en general
usando variables:
|
Multiplicar en
cruz es ir de esto: |
|
|
|
|
|
A esto: |
ad = bc
|
|
Recuerda...
multiplicar "en cruz":
|
 |
Ejemplo
Multiplicar en cruz puede
llevarte más rápido a la solución. Como en este ejemplo:
|
Calcula "x": |
|
|
|
|
|
Multiplicamos en
cruz: |
x2 = 8 × 2
|
|
|
|
|
Y resolvemos |
x = √16 = 4 |
Cuidado: cero
¡Ten cuidado! No puedes
usar esto si alguno de los denominadores ("b" y "d" en
la fórmula) es cero. Dividir entre cero es "ilegal"
Sigue
>>>Polinomios>>>

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
|