|
|
Exponentes

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
Entrar a exámenes
de:
Contenido Revisado 
|
|
|
Los exponentes también se llaman
potencias o
índices
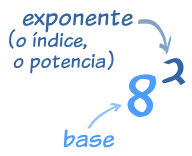 |
El exponente de un
número nos dice cuántas
veces se usa el número
en una multiplicación.
En este ejemplo: 82
= 8 × 8 = 64
-
En palabras: 82
se puede leer "8 a la
segunda potencia", "8 a
la potencia 2" o
simplemente "8 al
cuadrado"
|
Más
ejemplos:
Ejemplo: 53
= 5 × 5 × 5 = 125
-
En
palabras: 53 se puede
leer "5 a la tercera potencia",
"5 a la potencia 3" o
simplemente "5 al cubo"
Ejemplo: 24
= 2 × 2 × 2 × 2 = 16
-
En
palabras: 24 se puede
leer "2 a la cuarta potencia" or
"2 a la potencia 4" o
simplemente "2 a la cuarta"
Y los
exponentes hacen más fácil escribir
muchas multiplicaciones
Ejemplo: 96 es más
fácil de escribir y leer que
9 × 9 × 9 × 9 × 9
× 9
Puedes
multiplicar cualquier número por
sí mismo tantas veces como
quieras con esta notación.
Así que,
en general:
an
te dice que multipliques a
por sí mismo,
y hay n de esos a's: |
|
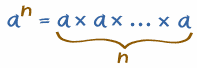 |
Exponentes negativos
¿Negativos?
¿Qué es lo contrario de multiplicar? ¡Dividir!
Un exponente negativo significa cuántas
veces se divide entre el número.
Ejemplo: 8-1
= 1 ÷ 8 = 0.125
O
varias divisiones:
Ejemplo: 5-3
= 1 ÷ 5 ÷ 5 ÷ 5 = 0.008
Pero
esto lo podemos hacer más fácilmente:
5-3
también se podría calcular así:
1 ÷ (5 × 5 × 5) = 1/53
= 1/125 = 0.008
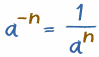 |
Este último ejemplo nos muestra
una manera más fácil de manejar
exponentes negativos:
-
Calcula la potencia positiva
(an)
-
Después cacula el recíproco
(o sea
1/an)
|
Más
ejemplos:
|
Exponente negativo |
|
Recíproco del exponente
positivo |
|
Respuesta |
|
4-2 |
= |
1 / 42
|
= |
1/16 = 0.0625 |
|
10-3 |
= |
1 / 103
|
= |
1/1,000 = 0.001 |
¿Qué
pasa si el exponente es 1 o 0?
Si el
exponente es 1, entonces tienes el
número solo (por ejemplo 91
= 9)
Si el
exponente es 0, la respuesta es 1
(por ejemplo 90 = 1)
Tiene
sentido
Mi
método favorito es empezar con "1" y
multiplicar y o dividir tantas veces
como diga el exponente, y tendrás la
respuesta correcta, por ejemplo:
|
Ejemplo: potencias de 5 |
|
|
... etc... |
|
 |
|
52 |
1 × 5 × 5 |
25 |
|
51 |
1 × 5 |
5 |
|
50 |
1 |
1 |
|
5-1 |
1 ÷ 5 |
0.2 |
|
5-2 |
1 ÷ 5 ÷ 5 |
0.04 |
|
|
... etc... |
|
Si
miras esta tabla, verás que los
exponentes positivos, cero y
negativos son en realidad parte de
un mismo (y bastante sencillo)
patrón.
|
|
Exponentes
Negativos
A los
exponentes también se los llama
índices.
 |
El exponente de un número
nos dice cuántas veces
debemos usar ese número en
una multiplicación.
En este ejemplo: 82
= 8 × 8 = 64
-
En palabras: 82
se podría llamar "8
elevado al 2" o
simplemente "8 al
cuadrado".
|
Entonces,
en general:
|
an
te dice que multipliques a
por sí misma un número n
de veces: |
|
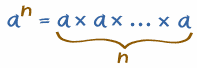 |
Pero
esos son exponentes positivos, ¿qué
pasa si tenemos algo como…?
8-2
Este
exponente es negativo ... ¿qué quiere
decir?
Exponentes Negativos
¿Negativo?
¿Qué puede ser lo opuesto a multiplicar?
¡Dividir!
La división
es la inversa (opuesta)
de la multiplicación.
Un
exponente negativo nos indica cuántas
veces dividir por ese número.
Por ejemplo:
8-1 = 1 ÷
8 = 1/8 = 0.125
O
muchas divisiones:
Por ejemplo:
5-3 = 1 ÷
5 ÷ 5 ÷ 5 = 0.008
Pero se
puede hacer de una forma más fácil:
5-3
también podría calcularse así:
1 ÷ (5 × 5 × 5) = 1/53
= 1/125 = 0.008
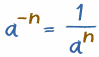 |
El
ultimo ejemplo nos mostró una
forma más simple de manejar
exponentes negativos:
-
Calcula el exponente (an)
-
Luego utiliza su Inverso (1/an)
|
Para
cambiar el signo (más a menos,
o menos a más) de el exponente usa
el Recíproco (es decir,
1/an)
Entonces,
¿cómo sería 8-2 ?
Por ejemplo:
8-2 = 1 ÷
8 ÷ 8 = 1/82 = 1/64 =
0.015625
Más
ejemplos:
|
Exponente negativo |
|
Inversa de un exponente
positivo |
|
Respuesta |
|
4-2 |
= |
1 / 42
|
= |
1/16 = 0.0625 |
|
10-3 |
= |
1 / 103
|
= |
1/1,000 = 0.001 |
Todo
Tiene Sentido
Mi
método favorito es comenzar con “1” y
luego multiplicar o dividir tantas veces
como el exponente me diga. Así obtendrás
la respuesta correcta, por ejemplo:
|
Ejemplo: Exponentes de 5 |
|
|
.. etc.. |
|
 |
|
52 |
1 × 5 × 5 |
25 |
|
51 |
1 × 5 |
5 |
|
50 |
1 |
1 |
|
5-1 |
1 ÷ 5 |
0.2 |
|
5-2 |
1 ÷ 5 ÷ 5 |
0.04 |
|
|
... etc... |
|
Si
miras esta tabla, verás que los
exponentes positivos, el cero o los
exponentes negativos son parte del
mismo modelo (bastante simple).
|
|
El
recíproco en álgebra
¡Dale la
vuelta!
El
recíproco de un número
Para tener el recíproco de un
número, sólo divide 1 entre
el número. |
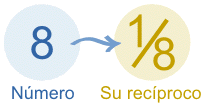 |
Ejemplos:
|
Número |
Recíproco |
En decimal |
|
2 |
1/2 |
= 0.5 |
|
8 |
1/8 |
= 0.125 |
|
1,000 |
1/1,000 |
= 0.001 |
Recíproco de una variable
Si
te dan una variable "x", su
recíproco es "1/x".
Igualmente, si te dan algo más
complicado como "x/y" entonces el
recíproco es sólo "y/x" (o sea, dale
la vuelta).
Ejemplo: ¿Cuál es el recíproco
de x/(x-1) ?
Respuesta: toma
x/(x-1) y
dale la vuelta: (x-1)/x
Notación
El
recíproco de "x" se indica así:
1/x
o
x-1
|
|
Cuadrados
y raíces cuadradas
Para
entender las raíces cuadradas primero
tienes que entender los cuadrados...
Cómo
se calcula el cuadrado de un número
Para
calcular el cuadrado de un número,
sólo hay que multiplicarlo por sí
mismo...
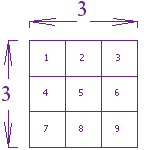
Ejemplo: ¿Cuál es el cuadrado de 3?
|
3
al cuadrado |
= |
 |
= |
3
× 3 |
= |
9 |
Nota: escribimos "3 al cuadrado"
como
32
(el "2"
pequeño significa que el número
aparece dos veces en la
multiplicación)
Más
cuadrados
|
4
al cuadrado |
= |
42 |
= |
4
× 4 |
= |
16 |
|
5
al cuadrado |
= |
52 |
= |
5
× 5 |
= |
25 |
|
6
al cuadrado |
= |
62 |
= |
6
× 6 |
= |
36 |
Raíz
cuadrada
La raíz
cuadrada va en la dirección
contraria:
3 al
cuadrado es 9, así que
la raíz cuadrada de 9 es
3
|
3 |
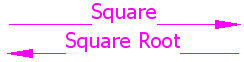 |
9 |
La raíz cuadrada de un
número es...
... ese valor particular
tal que cuando lo multiplicas por sí
mismo te da el número original.
La raíz cuadrada de 9
es ...
... 3, porque
cuando multiplicas 3 por sí mismo
sale 9.
 |
Nota: cuando veas "raíz" piensa
"conozco el árbol,
pero ¿cuál es la raíz que lo
produce?"
En
este caso el árbol es "9", y la
raíz es "3". |
Aquí
tienes más cuadrados y raíces cuadradas:
 |
|
4
|
|
16
|
|
5
|
|
25
|
|
6
|
|
36
|
Ejemplo: ¿Cuál es la raíz cuadrada
de 25?
Bueno, acabamos de ver que 25 = 5 ×
5, así que si multiplicas 5 por sí
mismo (5 × 5) sale 25.
Entonces la respuesta es 5
El
símbolo de raíz cuadrada
 |
Este es el símbolo que significa
"raíz cuadrada", es como una
marca de "correcto", de hecho
hace cientos de años empezó
siendo un punto con un palito
hacia arriba.
Se le llama radical,
¡y siempre hace que las
matemáticas parezcan importantes! |
Se usa
así:
 (se dice que "la raíz cuadrada de 9 es
3")
(se dice que "la raíz cuadrada de 9 es
3")
Abajo hay
temas más avanzados
También puedes calcular el cuadrado de
números negativos
Mira
esto:
|
El
cuadrado de 5 es 25: |
|
5
× 5 = 25 |
|
|
|
|
|
Pero el cuadrado de -5 también
es 25: |
|
-5
× -5 = 25 |
|
(porque
negativo por negativo es
positivo) |
|
|
Así que la
raíz cuadrada de 25 puede ser 5
o -5
¡Hay
una respuesta positiva y otra negativa
para una raíz cuadrada!
Pero
cuando la gente habla de "la" raíz
cuadrada normalmente se refieren a la
positiva.
Y
cuando usas el símbolo radical
√ siempre
quiere decir la raíz positiva.
Ejemplo:
√36 = 6 (no -6)
Cuadrados perfectos
Los
cuadrados perfectos son los cuadrados de
los números enteros:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
etc |
|
Cuadrados perfectos: |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
121 |
144 |
169 |
196 |
225 |
... |
Es
fácil calcular la raíz cuadrada de un
cuadrado perfecto, pero es muy
difícil calcular otras raíces
cuadradas.
Ejemplo: ¿cuál es la raíz cuadrada
de 10?
Bueno, 3 × 3 = 9 y 4 × 4 = 16, así
que podemos adivinar que la
respuesta está entre 3 y 4.
-
Probamos 3.5: 3.5 × 3.5 =
12.25
-
Probamos 3.2: 3.2 × 3.2 =
10.24
-
Probamos 3.1: 3.1 × 3.1 =
9.61
Así
vamos muy despacio... en este punto,
saco mi calculadora y veo que sale:
3.1622776601683793319988935444327
...
pero las cifras siguen y siguen, sin
patrón. ¡Así que incluso la
respuesta de la calculadora es
sólo una aproximación!
(Para saber más: este
tipo de números se llaman radicales
y son un tipo especial de números
irracionales)
Un
método especial para calcular una raíz
cuadrada
Hay
muchas maneras de calcular una raíz
cuadrada, pero mi favorita es una muy
sencilla que da una respuesta más exacta
cuantas más veces se usa:
a)
empieza
adivinando (digamos 4 para la
raíz cuadrada de 10)
b) divide entre tu
aproximación
(10/4 = 2.5)
c) suma eso a la
aproximación (2.5+4=6.5)
d) y divide eso entre 2, o
sea calcula la mitad. (6.5/2 = 3.25)
e) ahora, ese esa tu nueva
aproximación,
empieza otra vez en b)
... así
que nuestro primer intento nos lleva de
4 a 3.25
Otra vez (de b a e) nos da: 3.163
Otra vez (de b a e) nos da:
3.1623
Así que después de hacerlo tres veces la
respuesta es 3.1623, que está muy bien,
porque:
3.1623 x
3.1623 = 10.00014
Es
divertido hacer esto ... ¿por qué no lo
usas para calcular la raíz cuadrada de
2? |
|
Cubos y
raíces cúbicas
Para
entender las raíces cúbicas, primero
tienes que entender los cubos...
Cómo
calcular el cubo de un número
Para
hacer el cubo de un número,
sólo multiplícalo 3 veces ...
Ejemplo: ¿Cuánto es 3 al cubo?
|
3
al cubo |
= |
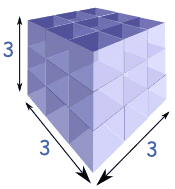 |
= |
3
× 3 × 3 |
= |
27 |
Nota: escribimos "3 al cubo" así:
33
(el "3"
pequeño dice que el número se
multiplica tres veces)
Algunos
cubos más
|
4
al cubo |
= |
43 |
= |
4
× 4 × 4 |
= |
64 |
|
5
al cubo |
= |
53 |
= |
5
× 5 × 5 |
= |
125 |
|
6
al cubo |
= |
63 |
= |
6
× 6 × 6 |
= |
216 |
Raíz
cúbica
La raíz
cúbica va en la otra dirección:
3 al
cubo es 27, así que
la raíz cúbica de 27 es 3
|
3 |
 |
27 |
La raíz cúbica de un
número es ...
... el valor exacto que,
al elevarlo al cubo, da el número
original.
La raíz cúbica de 27
es ...
... 3, porque
cuando hacemos el cubo de 3 nos da
27.
 |
Nota: cuando veas una "raíz"
piensa:
"conozco
el árbol, pero ¿cuál es la raíz
que lo ha producido?"
En
este caso el árbol es "27", y la
raíz cúbica es "3". |
Aquí
tienes más cubos y raíces cúbicas:
 |
|
4
|
|
64
|
|
5
|
|
125
|
|
6
|
|
216
|
Ejemplo: ¿Cuál es la raíz cúbica de
125?
Bueno, acabamos de ver que 125 =
5 × 5 × 5 (si multiplicas 5 tres
veces sale 125) ...
...
así que la respuesta es 5
El
símbolo de la raíz cúbica
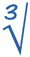 |
Este es el símbolo especial para
"raíces cúbicas", es el símbolo
"radical" (el de
las raíces cuadradas) con un
tres pequeño encima para indicar
que es una raíz cúbica. |
Se usa
así:
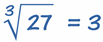 (se lee "la raíz cúbica de 27 es igual a
3")
(se lee "la raíz cúbica de 27 es igual a
3")
También puedes hacer la raíz cúbica de
números negativos
Mira
esto:
|
Si
haces el cubo de 5 sale 125: |
|
5
× 5 × 5 = 125 |
|
|
|
|
|
Si
haces el cubo de -5 sale -125: |
|
-5
× -5 × -5 = -125 |
Así que
la raíz cúbica de -125 es -5
Cubos
perfectos
Los
cubos perfectos son los cubos de los
números enteros:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
etc. |
|
Cubos perfectos: |
1 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
729 |
1000 |
1331 |
1728 |
2197 |
2744 |
3375 |
... |
Es
fácil calcular la raíz cúbica de un cubo
perfecto, pero es muy difícil
calcular otras raíces cúbicas.
Ejemplo: ¿cuál es la raíz cúbica de
30?
Bueno, 3 × 3 × 3 = 27 y 4 × 4 × 4 =
64, así que adivinamos que la
respuesta está entre 3 y 4.
-
Probamos con 3.5: 3.5 × 3.5 ×
3.5 = 42.875
-
Probamos con 3.2: 3.2 × 3.2 ×
3.2 = 32.768
-
Probamos con 3.1: 3.1 × 3.1 ×
3.1 = 29.791
Nos
vamos acercando, pero despacito ...
ahora saco la calculadora, ella me
dice:
3.1072325059538588668776624275224
...
pero las cifras siguen y siguen sin
que haya ningún patrón. ¡Así que la
respuesta de la calculadora sólo
es una aproximación !
|
|
Raíces n-ésimas
La "raíz
n-ésima" de un valor dado, cuando se
multiplica n veces da el valor
inicial
" n-ésima
"
1ª, 2ª,
3ª, 10ª (décima), 20ª
(vigésima), ... n-ésima ...
En vez
de hablar de la "4ª (cuarta)", "16ª (decimosexta)",
etc. , si queremos hablar en general
decimos la "n-ésima".
La
raíz n-ésima
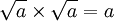 |
Así como la raíz cuadrada
es lo que se multiplica dos
veces para tener el valor
original... |
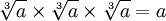 |
... y la raíz cúbica es
lo que se multiplica tres
veces para tener el valor
original... |
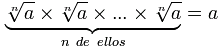 |
... la raíz n-ésima es lo
que se multiplica n veces
para tener el valor original |
Así
que es la manera general de
hablar de raíces
(podría ser la segunda, novena, 324ª
o cualquier otra)
El
símbolo de la raíz n-ésima
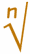 |
Este es el símbolo especial que
significa "raíz n-ésima", es el
símbolo "radical"
(el de las raíces cuadradas) con
una n pequeña para
indicar la raíz n-ésima. |
Uso
Se
podría usar la raíz n-ésima en una
pregunta así:
Pregunta:
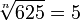 , ¿cuánto es "n"?
, ¿cuánto es "n"?
Respuesta: 5 × 5 × 5 × 5 = 625,
así que n=4 (es decir 5 se
usa 4 en la multiplicación)
O
podríamos usar "n" porque queremos
hablar de algo en general:
Ejemplo: Si n es impar
entonces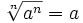
¿Por
qué "raíz"... ?
 |
Cuando cuando veas "raíz" piensa
"conozco el árbol,
pero ¿cuál es la raíz que lo
produce?"
En
el caso de √9 = 3 el
árbol es "9", y la raíz es 3. |
Propiedades
Ahora
que sabemos lo que es una raíz n-ésima,
veamos algunas propiedades:
Multiplicación y división
Puedes
"separar" así multiplicaciones dentro de
la raíz:
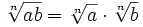
(suponemos que
a y b son ≥ 0)
Esto te
ayudará a simplificar ecuaciones en
álgebra, y también algunos cálculos:
Ejemplo:
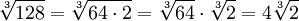
También
funciona con la división:
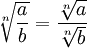
(a≥0 y b>0)
(b no puede ser cero porque no se puede
dividir entre cero)
Ejemplo:
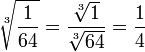
Suma y
restas
¡Pero
no se puede hacer lo mismo con
sumas y restas!
Es
fácil caer en la trampa, así que ten
cuidado. También quiere decir que
desgraciadamente las sumas y restas son
más difíciles cuando están dentro de una
raíz.
Exponentes y raíces
Un
exponente a un lado del "=" se convierte
en una raíz cuando se pasa al otro lado
del "=":
 |
Si
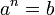 entonces
entonces
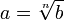 (b ≥
0)
(b ≥
0) |
|
|
|
Ejemplo:
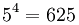 entonces
entonces
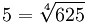
|
|
Raíz
n-ésima de una potencia n-ésima
Cuando
un valor tiene un exponente n y
calculas su raíz n-ésima,
recuperas el valor del principio (o a
veces su valor absoluto):
|
|
|
Ejemplos |
 |
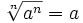 (si a ≥ 0)
(si a ≥ 0)
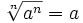 (para cualquier a, si
n es impar)
(para cualquier a, si
n es impar)
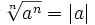 (para
cualquier a, si n es
par) (para
cualquier a, si n es
par)
(Nota: |a| quiere decir
el valor absoluto de a) |
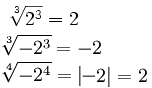
|
Raíz
n-ésima de una potencia m-ésima
Ahora
vemos qué pasa cuando el exponente y la
raíz tienen valores diferentes (m
y n).
Así que...
puedes poner el exponente "dentro" de la
raíz n-ésima, cosa que a veces es útil.
Pero
hay otro método todavía más poderoso...
puedes combinar el exponente y la raíz
para hacer un nuevo exponente, así:
Es
porque la raíz n-ésima es lo
mismo que el exponente (1/n):
 |
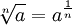 |
Ejemplo: 2½
= √2 (la raíz cuadrada de
2) |
|
|
Radicales
Cuando
no puedes simplificar un número para
quitar una raíz cuadrada (o una raíz
cúbica, etc.) entonces es un radical.
Ejemplo:
√2 (la raíz cuadrada de 2) no se puede
simplificar más así que es un radical.
Pero √4
(la raíz cuadrada de 4) sí se
puede simplificar (queda 2), así que
no es un radical.
Fíjate
en estos:
|
Número |
Simplificado |
En decimal |
¿Radical
o no? |
|
√2 |
√2 |
1.4142135(etc) |
Radical |
|
√3 |
√3 |
1.7320508(etc) |
Radical |
|
√4 |
2 |
2 |
No es radical |
|
√(1/4) |
1/2 |
0.5 |
No es radical |
|
3√(11) |
3√(11) |
2.2239800(etc) |
Radical |
|
3√(27) |
3 |
3 |
No es radical |
|
5√(3) |
5√(3) |
1.2457309(etc) |
Radical |
Como
ves, los radicales tienen infinitas
cifras decimales que no se repiten nunca,
y por eso son números irracionales.
 |
De
hecho "radical" se refiere en
concreto a una raíz que
es irracional. |
 |
Alrededor del año 820 AC,
al-Khwarizmi (el matemático
persa de cuyo nombre viene la
palabra "Algoritmo") decía que
los números irracionales eran "inaudibles"
... esto se tradujo al latín
como surdus ("sordo"
o "mudo") |
Conclusión
Si es
una raíz e irracional,
es un radical.
Pero
no todas las raíces son
radicales.
|
|
Exponentes
fraccionarios
También se llaman
"radicales"
Exponentes
 |
El exponente de un número
dice cuántas veces se
multiplica el número.
En este ejemplo: 82
= 8 × 8 = 64
-
En palabras: 82
se puede leer "8 a la
segunda potencia", "8 a
la potencia 2" o
simplemente "8 al
cuadrado"
|
Exponentes fraccionarios: ½
En el
ejemplo de arriba, el exponente es "2",
¿pero y si fuera "½"? ¿Cómo funcionaría?
Pregunta: ¿Qué es x½ ?
Respuesta: x½ = la raíz
cuadrada de x (o sea x½
= √x)
¿Por
qué?
Porque si
calculas el cuadrado de x½
tienes: (x½)2 = x1
= x
Para
entenderlo, sigue esta explicación de
dos pasos:
|
1 |
Primero, hay una regla
general: (xm)n
= xm×n
(Porque primero
multiplicas x "m" veces,
después tienes que hacer
eso "n" veces, en total
m×n veces)
Ejemplo: (x2)3
= (xx)3 = (xx)(xx)(xx)
= xxxxxx = x6
Así que (x2)3
= x2×3 = x6 |
|
2 |
Ahora, vemos qué pasa cuando
hacemos el cuadrado
de x½:
(x½)2
= x½×2 = x1
= x
Cuando hacemos el
cuadrado de x½
sale x, así x½
tiene que ser la raíz
cuadrada de x
|
Probamos con otra fracción
Vamos a
probar otra vez, pero con un exponente
de un cuarto (1/4):
¿Qué
es x¼?
(x¼)4
= x¼×4 = x1 =
x
Entonces, ¿qué valor
se puede multiplicar 4 veces para
tener x? Respuesta:
La raíz cuarta de x.
Así que x¼ = la raíz
cuarta de x
Regla
general
De
hecho podemos hacer una regla general:
 |
|
Un exponente
fraccionario como
1/n significa
hacer la raíz n-ésima: |
 |
|
Ejemplo: ¿Cuánto es 271/3
?
Respuesta: 271/3 =
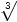 27
= 3 27
= 3
¿Qué
pasa con fracciones más complicadas?
Las
fracciones más complicadas se pueden
separar en dos partes:
-
una parte con un número entero,
y
-
una parte con una fracción del
tipo 1/n
Para entender eso, sólo recuerda que
m/n = m × (1/n):
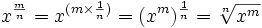
Así
que tenemos esto:
 |
|
Un
exponente
fraccionario como
m/n significa
haz la potencia
m-ésima, después
haz
la raíz n-ésima |
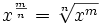 |
|
Ejemplo: ¿Cuánto es 43/2
?
Respuesta: 43/2 = 43×(1/2)
= √(43) = √(4×4×4) =
√(64) = 8
|
|
Leyes de
los exponentes
Los exponentes también se
llaman potencias o
índices
 |
El exponente de un número
dice cuántas veces se
multiplica el número.
En este ejemplo: 82
= 8 × 8 = 64
-
En palabras: 82
se puede leer "8 a la
segunda potencia", "8 a
la potencia 2" o
simplemente "8 al
cuadrado"
|
Todo lo que necesitas saber...
Todas
las "Leyes de los Exponentes" (o también
"reglas de los exponentes") vienen de
tres ideas:
 |
El
exponente de un número dice
multiplica el número por sí
mismo tantas veces |
|
|
|
 |
Lo contrario de
multiplicar es dividir, así que
un
exponente negativo significa
dividir |
|
|
|
 |
|
Un exponente
fraccionario como 1/n
quiere decir
hacer la raíz n-ésima: |
 |
|
Si
entiendes esto, ¡entonces entiendes
todos los exponentes!
Y todas
las reglas que siguen se basan en esas
ideas.
Leyes
de los exponentes
Aquí
están las leyes (las explicaciones están
después):
|
Ley |
Ejemplo |
|
x1 = x |
61 = 6 |
|
x0 = 1 |
70 = 1 |
|
x-1 = 1/x |
4-1 = 1/4 |
| |
|
|
xmxn
= xm+n |
x2x3
= x2+3 = x5 |
|
xm/xn
= xm-n |
x4/x2
= x4-2 = x2 |
|
(xm)n
= xmn |
(x2)3
= x2×3 = x6 |
|
(xy)n
= xnyn |
(xy)3
= x3y3 |
|
(x/y)n
= xn/yn |
(x/y)2
= x2 / y2 |
|
x-n
= 1/xn |
x-3
= 1/x3 |
| |
|
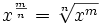 |
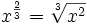 |
Explicaciones de las leyes
Las
tres primeras leyes (x1
= x, x0
= 1 y x-1
= 1/x) son sólo parte de la
sucesión natural de exponentes. Mira
este ejemplo:
|
Ejemplo: potencias de 5 |
|
|
... etc... |
|
 |
|
52 |
1 × 5 × 5 |
25 |
|
51 |
1 × 5 |
5 |
|
50 |
1 |
1 |
|
5-1 |
1 ÷ 5 |
0.2 |
|
5-2 |
1 ÷ 5 ÷ 5 |
0.04 |
|
|
... etc... |
|
verás
que los exponentes positivos, cero y
negativos son en realidad parte de un
mismo patrón, es decir 5 veces más
grande (o pequeño) cuando el exponente
crece (o disminuye).
La ley que dice que xmxn
= xm+n
En xmxn,
¿cuántas veces multiplicas "x"?
Respuesta: primero "m" veces,
despuésotras "n" veces, en total
"m+n" veces.
Ejemplo: x2x3 =
(xx) × (xxx) = xxxxx = x5
Así
que x2x3 = x(2+3)
= x5
La ley que dice que xm/xn
= xm-n
Como en el
ejemplo anterior, ¿cuántas veces
multiplicas "x"? Respuesta: "m" veces,
después reduce eso "n" veces (porque
estás dividiendo), en total "m-n" veces.
Ejemplo: x4-2 = x4/x2
= (xxxx) / (xx) = xx = x2
(Recuerda
que x/x = 1, así que cada vez que hay
una x "sobre la línea" y una "bajo la
línea" puedes cancelarlas.)
Esta
ley también te muestra por qué x0=1
:
Ejemplo: x2/x2
= x2-2
= x0 =1
La ley que dice que (xm)n
= xmn
Primero
multiplicas x "m" veces. Después tienes
que hacer eso "n" veces, en total
m×n veces.
Ejemplo: (x3)4 =
(xxx)4 = (xxx)(xxx)(xxx)(xxx)
= xxxxxxxxxxxx = x12
Así
que (x3)4 = x3×4
= x12
La ley que dice que (xy)n = xnyn
Para ver
cómo funciona, sólo piensa en ordenar
las "x"s y las "y"s como en este ejemplo:
Ejemplo: (xy)3 = (xy)(xy)(xy)
= xyxyxy = xxxyyy = (xxx)(yyy) = x3y3
La ley que dice que (x/y)n =
xn/yn
Parecido
al ejemplo anterior, sólo ordena las "x"s
y las "y"s
Ejemplo: (x/y)3 = (x/y)(x/y)(x/y)
= (xxx)/(yyy) = x3/y3
La ley
que dice que
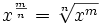
Para
entenderlo, sólo recuerda de las
fracciones que n/m = n × (1/m):
Ejemplo:
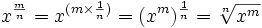
Y
eso es todo
Si te cuesta recordar
todas las leyes, acuérdate de esto:
siempre puedes
calcular todo si entiendes las tres
ideas de la parte de arriba de esta
página.
Ah,
una cosa más... ¿Qué pasa si x= 0?
|
Exponente positivo (n>0) |
0n
= 0 |
|
Exponente negativo (n<0) |
¡No definido!
(Porque dividimos entre 0) |
|
Exponente = 0 |
Ummm ...
¡lee más abajo! |
El extraño caso de 00
Hay dos
argumentos diferentes sobre el valor
correcto. 00 podría ser 1, o
quizás 0, así que alguna gente dice que
es "indeterminado":
 |
x0
= 1, así que ... |
00
= 1 |
|
0n
= 0, así que ... |
00
= 0 |
|
Cuando dudes... |
00 =
"indeterminado" |
|
|
Variables
con exponentes
Cómo
multiplicarlas y dividirlas
 |
Un
exponente (como el 2 en x2)
dice cuántas veces se usa la
variable en una multiplicación. |
Ejemplo: y2 = yy
(esto
es y multiplicado por y,
porque en Álgebra poner dos letras
juntas significa multiplicarlas)
Igualmente z3 = zzz
y x5
= xxxxx
Exponente 1
Si el
exponente es 1, la variable está sola (por
ejemplo x1 = x)
Normalmente no escribimos el "1", pero a
veces ayuda recordar que x
también es x1
Exponente 0
Si el
exponente es 0, entonces no estás
multiplicando nada y la respuesta es
sólo "1" (por ejemplo y0
= 1)
Multiplicar variables con exponentes
Entonces, cómo multiplicas esto:
(y2)(y3)
Sabemos
que y2 = yy, y y3
= yyy así que lo escribimos todo:
y2
y3 =
yyyyy
Eso son
5 "y"s multiplicadas juntas, así que el
nuevo exponente es 5:
y2
y3 = y5
¿Pero para
qué contar las "y"s cuando los
exponentes ya nos dicen cuántas hay?
Los
exponentes nos dicen que hay dos "y"s
multiplicadas por 3 "y"s que hacen un
total de 5 "y"s:
y2
y3
= y2+3
=
y5
¡Así
que el método más simple es sumar los
exponentes! (Nota: esa es sólo una
de las Leyes de los Exponentes)
|
|
Sigue
>>>Simplificar>>>

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
|